Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(4a\), \(SA\) vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left(SBC\right)\) và mặt phẳng đáy bằng \(60^\circ\). Diện tích của mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng
| \(\dfrac{172\pi a^2}{3}\) | |
| \(\dfrac{76\pi a^2}{3}\) | |
| \(84\pi a^2\) | |
| \(\dfrac{172\pi a^2}{9}\) |
Chọn phương án A.
Gọi \(O\) là tâm đường tròn ngoại tiếp \(\triangle ABC\), \(H\) là trung điểm của cạnh \(BC\).
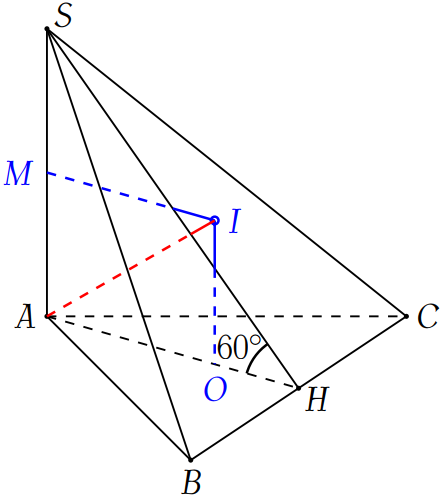
Vì \(\triangle ABC\) đều (cạnh \(4a\)) nên \(AH=4a\cdot\dfrac{\sqrt{3}}{2}=2a\sqrt{3}\) và \(OA=\dfrac{2}{3}AH=\dfrac{4a\sqrt{3}}{3}\).
Theo đề bài ta có $$\left((SBC),(ABC)\right)=\left(SH,AH\right)=\widehat{SHA}=60^\circ$$
Xét tam giác vuông \(SAH\) ta có $$\tan\widehat{SHA}=\dfrac{SA}{AH}=\dfrac{SA}{2\sqrt{3}a}=\sqrt{3}$$Suy ra \(SA=6a\).
Gọi \(d_1\) là trục của \(\triangle ABC\), dễ thấy \(d_1\subset(SAH)\).
Trong mặt phẳng \((SAH)\), kẻ đường trung trực \(d_2\) của đoạn thẳng \(SA\).
Gọi \(M\) là trung điểm của cạnh \(SA\), \(I\) là giao điểm của \(d_1\) và \(d_2\).
- Vì \(I\in d_1\) nên \(IA=IB=IC\).
- Vì \(I\in d_2\) nên \(IA=IS\).
Vậy \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\), với bán kính $$\begin{aligned}R&=\sqrt{IM^2+MA^2}\\ &=\sqrt{\left(\dfrac{4a\sqrt{3}}{3}\right)^2+(3a)^2}\\ &=\dfrac{\sqrt{129}}{3}a.\end{aligned}$$
Diện tích mặt cầu cần tìm là $$\begin{aligned}S&=4\pi{R^2}=4\pi\left(\dfrac{\sqrt{129}}{3}a\right)^2\\ &=\dfrac{172\pi{a^2}}{3}.\end{aligned}$$
