Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\ln\big(x^2-2x+m+1\big)$ có tập xác định là $\mathbb{R}$.
| $m=0$ | |
| $m< -1$ hoặc $m>0$ | |
| $m>0$ | |
| $0< m< 3$ |
Tìm tập xác định của hàm số $y=\log_{2023}\big(3x-x^2\big)$.
| $\mathscr{D}=(0;+\infty)$ | |
| $\mathscr{D}=(-\infty;0)\cup(3;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(0;3)$ |
Cho hàm số $f(x)=\ln\big(x^2+1\big)$. Giá trị $f'(2)$ bằng
| $\dfrac{4}{5}$ | |
| $\dfrac{4}{3\ln2}$ | |
| $\dfrac{4}{2\ln5}$ | |
| $2$ |
Cho số thực $m$ sao cho đường thẳng $x=m$ cắt đồ thị hàm số $y=\log_2x$ tại $A$ và đồ thị hàm số $y=\log_2(x+3)$ tại $B$ thỏa mãn $AB=3$. Khẳng định nào dưới đây đúng?
| $m\in\left(\dfrac{1}{3};\dfrac{1}{2}\right)$ | |
| $m\in\left(0;\dfrac{1}{3}\right)$ | |
| $m\in\left(\dfrac{2}{3};1\right)$ | |
| $m\in\left(\dfrac{1}{2};\dfrac{2}{3}\right)$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Tập xác định của hàm số $y=\log_{2022}(2x-1)$ là
| $[0;+\infty)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ | |
| $\left[\dfrac{1}{2};+\infty\right)$ | |
| $(0;+\infty)$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
Đạo hàm của hàm số $y=\log_2(x-1)$ là
| $y'=\dfrac{x-1}{\ln2}$ | |
| $y'=\dfrac{1}{\ln2}$ | |
| $y'=\dfrac{1}{(x-1)\ln2}$ | |
| $y'=\dfrac{1}{x-1}$ |
Tập xác định của hàm số $y=\ln(2-x)$ là
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(-\infty;2)$ | |
| $\mathscr{D}=(2;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}\setminus\{2\}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=\log_3x$ là
| $y'=\dfrac{1}{x}$ | |
| $y'=\dfrac{1}{x\ln3}$ | |
| $y'=\dfrac{\ln3}{x}$ | |
| $y'=-\dfrac{1}{x\ln3}$ |
Tiệm cận ngang của đồ thị hàm số $y=3^x$ và tiệm cận đứng của đồ thị hàm số $y=\log_2x$ lần lượt có phương trình là
| $y=3$ và $x=0$ | |
| $x=0$ và $y=0$ | |
| $y=0$ và $x=2$ | |
| $y=0$ và $x=0$ |
Tính đạo hàm của hàm số $y=2x^3+x\ln x$ tại điểm $x=1$.
| $6$ | |
| $2$ | |
| $3$ | |
| $7$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Có bao nhiêu số nguyên thuộc tập xác định của hàm số $y=\log\big[(6-x)(x+2)\big]$?
| $7$ | |
| $8$ | |
| $9$ | |
| Vô số |
Tập xác định của hàm số $y=\log_3(x-4)$ là
| $(5;+\infty)$ | |
| $(-\infty;+\infty)$ | |
| $(4;+\infty)$ | |
| $(-\infty;4)$ |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\log_2\left(x^2-2x+m\right)$ có tập xác định là $\mathbb{R}$.
| $m\geq1$ | |
| $m\leq1$ | |
| $m>1$ | |
| $m< -1$ |
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án $A,\,B,\,C,\,D$ dưới đây.
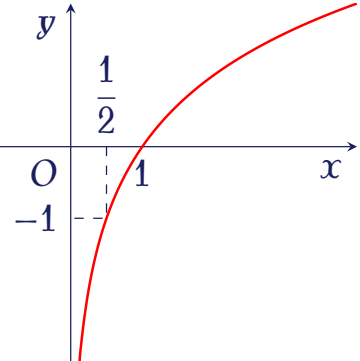
Hỏi hàm số đó là hàm số nào?
| $y=\log_2x$ | |
| $y=\log_{\sqrt{2}}x$ | |
| $y=\log_22x$ | |
| $y=\log_{\tfrac{1}{2}}x$ |
Hàm số nào dưới dây là hàm số đồng biến trên $\mathbb{R}$?
| $y=\left(\sqrt{2}-1\right)^x$ | |
| $y=\log_3x$ | |
| $y=\left(\dfrac{1}{3}\right)^x$ | |
| $y=3^x$ |
