Tìm giá trị nhỏ nhất của hàm số $y=2\sqrt{x+2}$ trên đoạn $[-1;3]$.
| $1$ | |
| $2$ | |
| $4$ | |
| $-1$ |
Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Tìm giá trị nhỏ nhất của hàm số $y=x+\dfrac{3}{x}-4$ trên đoạn $[1;5]$.
| $\dfrac{8}{5}$ | |
| $4-2\sqrt{3}$ | |
| $0$ | |
| $2\sqrt{3}-4$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Cho mặt cầu $\mathscr{S}(O,r)$, biết khoảng cách từ $O$ tới mặt phẳng $(P)$ bằng $\dfrac{r}{3}$. Mặt phẳng $(P)$ cắt mặt cầu theo một đường tròn có bán kính bằng
| $\dfrac{2r\sqrt{2}}{3}$ | |
| $r\sqrt{3}$ | |
| $\dfrac{2r}{3}$ | |
| $\dfrac{r\sqrt{3}}{3}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
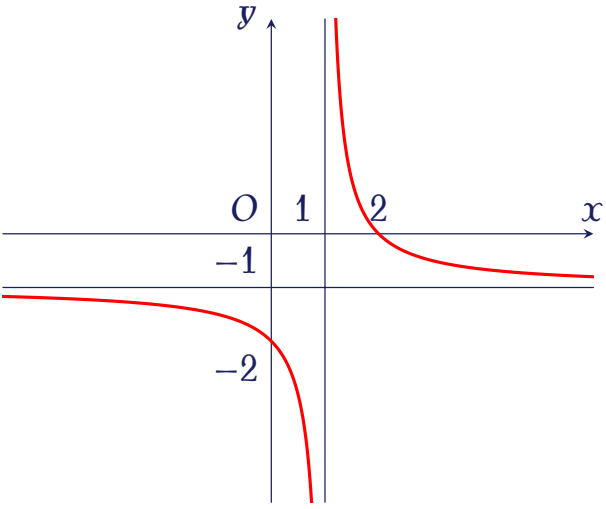
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Phương trình $3^{1-x}=9$ có nghiệm là
| $x=-1$ | |
| $x=-2$ | |
| $x=1$ | |
| $x=2$ |
Tập nghiệm của bất phương trình $3^x>5$ là
| $\big(0;\log_35\big)$ | |
| $\big(\log_53;+\infty\big)$ | |
| $\big(\log_35;+\infty\big)$ | |
| $\big(0;\log_53\big)$ |
Cho khối nón có diện tích đáy $B=a^2$ và chiều cao $h=3a$. Thể tích của khối nón bằng
| $a^3$ | |
| $3a^3$ | |
| $2a^3$ | |
| $4a^3$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho số thực $a>0$ và $a\neq1$, khi đó $\log_a\sqrt[3]{a}$ bằng
| $-\dfrac{1}{3}$ | |
| $\dfrac{1}{3}$ | |
| $-3$ | |
| $3$ |
Cho hai số thực $a,\,b>1$. Khẳng định nào dưới đây đúng?
| $\log(a+b)=\log a+\log b$ | |
| $\log(ab)=\log a+\log b$ | |
| $\log(a-b)=\log a-\log b$ | |
| $\log\left(\dfrac{a}{b}\right)=\log a+\log b$ |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=3x^3-x$ | |
| $y=-2x^4-x$ | |
| $y=-2x^3+3$ | |
| $y=-x^4+2$ |
Phương trình $\log_2(x+1)=3$ có nghiệm là
| $x=9$ | |
| $x=6$ | |
| $x=7$ | |
| $x=8$ |
Cho phương trình $9^x-2\cdot3^{x+2}-1=0$. Đặt $t=3^x$, $t>0$, phương trình đã cho trở thành phương trình nào dưới đây?
| $2t^2-9t-2=0$ | |
| $t^2-9t-1=0$ | |
| $t^2-18t-1=0$ | |
| $9t^2-2t-9=0$ |
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, $AA'=2a$. Một khối trụ có hai đáy là hai đường tròn ngoại tiếp hai tam giác $ABC.A'B'C'$. Thể tích của khối trụ đó bằng
| $\dfrac{4\pi a^3}{3}$ | |
| $\pi a^3$ | |
| $\dfrac{2\pi a^3}{3}$ | |
| $\dfrac{\pi a^3}{3}$ |
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau:
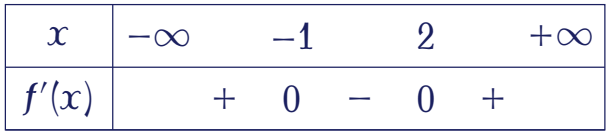
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
| $(-\infty;2)$ | |
| $(-\infty;-1)$ | |
| $(1;2)$ | |
| $(-1;+\infty)$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
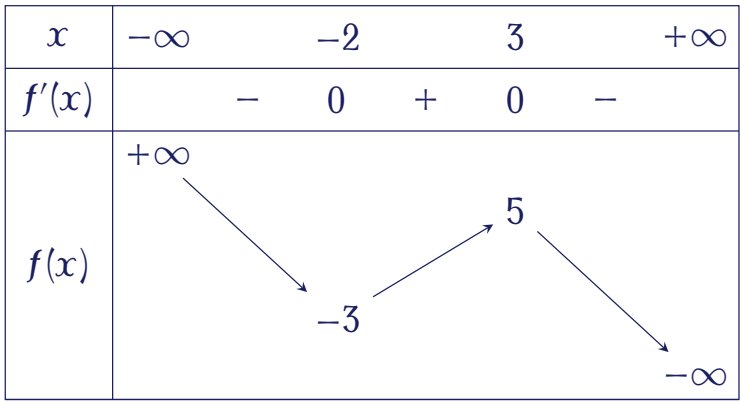
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
Cho hai số thực $x,\,y$ bất kì. Khẳng định nào dưới đây đúng?
| $5^x< 5^y\Leftrightarrow x>y$ | |
| $5^x>5^y\Leftrightarrow x>y$ | |
| $5^x>5^y\Leftrightarrow x< y$ | |
| $5^x>5^y\Leftrightarrow x=y$ |
Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?
| $y=x^3-2x^2-1$ | |
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^4+2x^2+1$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Cho các số thực dương $a,\,b$ thỏa mãn $9^{\log_3\big(ab^2\big)}=4ab^3$. Tích $ab$ bằng
| $4$ | |
| $2$ | |
| $3$ | |
| $6$ |
Cho hình trụ có độ dài đường sinh $\ell$ và bán kính đáy $3r$. Diện tích xung quanh của hình trụ bằng
| $\pi r\ell$ | |
| $4\pi r\ell$ | |
| $2\pi r\ell$ | |
| $6\pi r\ell$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=\mathrm{e}^x$ | |
| $y=\big(\sqrt{2}\big)^x$ | |
| $y=\left(\dfrac{4}{3}\right)^x$ | |
| $y=\left(\dfrac{1}{3}\right)^x$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Cho khối cầu có bán kính $r=\sqrt{3}$. Thể tích của khối cầu bằng
| $9\pi$ | |
| $\dfrac{4\pi}{3}$ | |
| $2\pi\sqrt{3}$ | |
| $4\pi\sqrt{3}$ |
Cho khối đa diện có tất cả các mặt đều là ngũ giác. Kí hiệu M là số mặt, C là số cạnh của khối đa diện. Khẳng định nào dưới đây đúng?
| $5M=C$ | |
| $5M=2C$ | |
| $2M=3C$ | |
| $3M=2C$ |
Trong không gian cho tam giác $ABC$ vuông tại $A$, $AB=2a$, $AC=3a$. Khi quay tam giác $ABC$ quanh cạnh $AB$ thì đường gấp khúc $ACB$ tạo thành một hình nón. Độ dài đường sinh của hình nón đó là
| $a\sqrt{13}$ | |
| $a\sqrt{5}$ | |
| $2a$ | |
| $3a$ |
$\lim\limits_{x\to0}\dfrac{\mathrm{e}^x-1}{3x}$ bằng
| $0$ | |
| $1$ | |
| $3$ | |
| $\dfrac{1}{3}$ |
Tập nghiệm của phương trình $\log_2(x-1)+\log_2(x+3)=3$ là
| $\left\{-1+2\sqrt{3}\right\}$ | |
| $\left\{-1+2\sqrt{3};-1-2\sqrt{3}\right\}$ | |
| $\left\{-1+\sqrt{10}\right\}$ | |
| $\left\{-1+\sqrt{10};-1-\sqrt{10}\right\}$ |
Gọi $x_1,\,x_2$ là các điểm cực trị của hàm số $y=x^3-2x^2-7x+1$. Tính $x_1^2+x_2^2$.
| $\dfrac{44}{9}$ | |
| $\dfrac{16}{3}$ | |
| $\dfrac{28}{3}$ | |
| $\dfrac{58}{9}$ |
Cho các số thực dương $x,\,y$ thỏa mãn $\ln x+\ln y\geq\ln\big(2x+y^2\big)$. Tìm giá trị nhỏ nhất của biểu thức $S=x+8y$.
| $32$ | |
| $29$ | |
| $25$ | |
| $46$ |
Cho khối chóp tứ giác $S.ABCD$ có thể tích $V$ và đáy là hình bình hành. Gọi $N$ là điểm trên cạnh $SD$ sao cho $ND=2NS$. Một mặt phẳng chứa $BN$ và song song với $AC$, cắt $SA,\,SC$ lần lượt tại $P,\,Q$. Gọi $V'$ là thể tích của khối chóp $S.BPNQ$. Khẳng định nào dưới đây đúng?
| $\dfrac{V'}{V}=\dfrac{1}{6}$ | |
| $\dfrac{V'}{V}=\dfrac{2}{5}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{3}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{4}$ |
Cho các số thực $a>1$, $b>1$, $c>1$ thỏa mãn $\dfrac{2}{\log_ac^6}+\dfrac{3}{\log_bc^6}=\dfrac{1}{3}$. Đẳng thức nào dưới đây đúng?
| $a^2b^2=c^3$ | |
| $a^2b^3=c^2$ | |
| $a^3b^2=c^2$ | |
| $a^3b^2=c$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây:
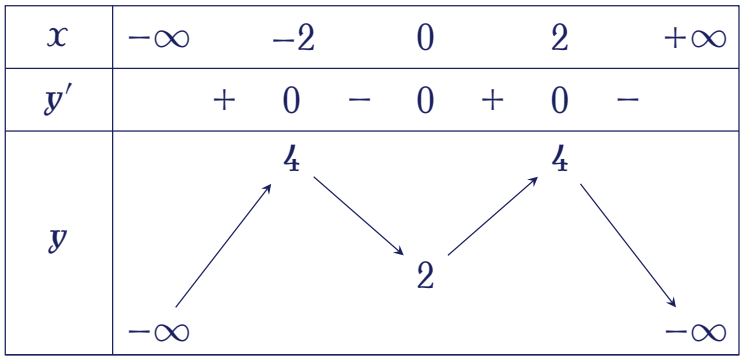
Số nghiệm của phương trình $f^2(x)-4f(x)+3=0$ là
| $5$ | |
| $3$ | |
| $6$ | |
| $4$ |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho hình trụ có bán kính đáy và chiều cao đều bằng $a$. Gọi $AB$, $CD$ là các dây cung của hai đường tròn đáy sao cho tứ giác $ABCD$ là hình vuông và mặt phẳng $ABCD$ không vuông góc với mặt phẳng đáy. Tính độ dài đoạn thẳng $AB$.
| $\dfrac{a\sqrt{5}}{3}$ | |
| $\dfrac{a\sqrt{5}}{2}$ | |
| $\dfrac{a\sqrt{10}}{2}$ | |
| $\dfrac{a\sqrt{10}}{3}$ |
Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$. Biết diện tích tứ giác $ABCD$ bằng ba lần diện tích tam giác $SAB$. Tính thể tích khối chóp đã cho.
| $\dfrac{a^3\sqrt{7}}{9}$ | |
| $\dfrac{a^3\sqrt{7}}{6}$ | |
| $\dfrac{a^3\sqrt{7}}{12}$ | |
| $\dfrac{a^3\sqrt{7}}{18}$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Gọi $x_1,\,x_2$ là các nghiệm của phương trình $2\log2+2\log(x+2)=\log x+4\log3$. Tích $x_1x_2$ bằng
| $\dfrac{15}{2}$ | |
| $\dfrac{9}{2}$ | |
| $6$ | |
| $4$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\{0;1\}$ | |
| $\{1\}$ | |
| $\{-1;1\}$ | |
| $\{0\}$ |
Cho số thực $m$ sao cho đường thẳng $x=m$ cắt đồ thị hàm số $y=\log_2x$ tại $A$ và đồ thị hàm số $y=\log_2(x+3)$ tại $B$ thỏa mãn $AB=3$. Khẳng định nào dưới đây đúng?
| $m\in\left(\dfrac{1}{3};\dfrac{1}{2}\right)$ | |
| $m\in\left(0;\dfrac{1}{3}\right)$ | |
| $m\in\left(\dfrac{2}{3};1\right)$ | |
| $m\in\left(\dfrac{1}{2};\dfrac{2}{3}\right)$ |
Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AB=3$, $AD=4$. Biết đường thẳng $SA$ vuông góc với mặt phẳng đáy và góc tạo bởi đường thẳng $SC$ và mặt phẳng đáy bằng $45^\circ$. Tính bán kính mặt cầu ngoại tiếp hình chóp $S.ABCD$.
| $\dfrac{5\sqrt{2}}{2}$ | |
| $\dfrac{5}{2}$ | |
| $\dfrac{2\sqrt{5}}{3}$ | |
| $\dfrac{5}{3}$ |
