Ngân hàng bài tập
A
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
1 lời giải
Chọn phương án A.
Vì $CC'\perp(ABC)$ nên $AC$ là hình chiếu vuông góc của $AC'$ trên mặt phẳng $(ABC)$. Do đó $\big(AC',(ABC)\big)=(AC',AC)=\widehat{C'AC}$.
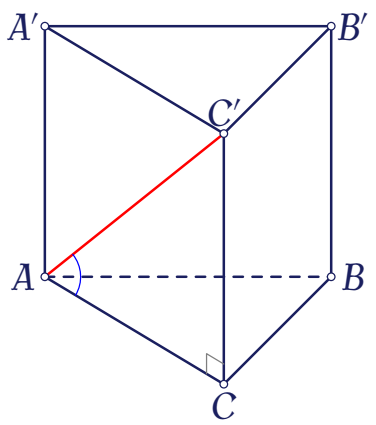
Trong tam giác vuông $ACC'$ ta có $$\tan\widehat{C'AC}=\dfrac{CC'}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}$$
Vậy $\widehat{C'AC}=60^\circ$.
