Gọi \(M\) và \(N\) là giao điểm của đồ thị hai hàm số \(y=x+1\) và \(y=\dfrac{2x+4}{x-1}\). Tìm hoành độ trung điểm \(I\) của đoạn thẳng \(MN\).
| \(x_I=-\dfrac{5}{2}\) | |
| \(x_I=2\) | |
| \(x_I=\dfrac{5}{2}\) | |
| \(x_I=1\) |
Đồ thị của hàm số $y=-x^4+4x^2-3$ cắt trục tung tại điểm có tung độ bằng
| $0$ | |
| $3$ | |
| $1$ | |
| $-3$ |
Giao điểm của hai parabol $y=x^2-4$ và $y=14-x^2$ là
| $M(2;10)$ và $N(-2;10)$ | |
| $M\left(\sqrt{14};10\right)$ và $N(-14;10)$ | |
| $M(3;5)$ và $N(-3;5)$ | |
| $M\left(\sqrt{18};14\right)$ và $M\left(-\sqrt{18};14\right)$ |
Parabol $\left(\mathscr{P}\right)\colon y=x^2+4x+4$ có số điểm chung với trục hoành là
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
Tọa độ giao điểm của parabol $\left(\mathscr{P}\right)\colon y=x^2-4x$ với đường thẳng $d\colon y=-x-2$ là
| $M(-1;-1)$, $N(-2;0)$ | |
| $M(1;-3)$, $N(2;-4)$ | |
| $M(0;-2)$, $N(2;-4)$ | |
| $M(-3;1)$, $N(3;-5)$ |
Tọa độ giao điểm của parabol $\left(P\right)\colon y=x^2-4x$ và đường thẳng $d\colon y=-x-2$ là
| $M\left(-1;-1\right)$, $N\left(-2;0\right)$ | |
| $M\left(1;-3\right)$, $N\left(2;-4\right)$ | |
| $M\left(0;-2\right)$, $N\left(2;-4\right)$ | |
| $M\left(-3;1\right)$, $N\left(3;-5\right)$ |
Điểm nào sau đây là điểm chung của parabol \(y=x^2-x+1\) và đường thẳng \(y=2x-1\)?
| \(P(3;5)\) | |
| \(N(2;3)\) | |
| \(M(1;-1)\) | |
| \(Q(0;1)\) |
Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol \((P)\colon y=x^2\) và đường thẳng \(d\colon y=x\) xoay quanh trục \(Ox\) bằng
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x-\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}x^2\mathrm{\,d}x+\pi\displaystyle\int\limits_{0}^{1}x^4\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)^2\mathrm{\,d}x\) | |
| \(\pi\displaystyle\int\limits_{0}^{1}\left(x^2-x\right)\mathrm{\,d}x\) |
Tìm tọa độ giao điểm của parabol \(y=-x^2+2x+1\) với đường thẳng \(y=2x-3\).
| \((2;1)\) | |
| \((2;-2)\) và \((1;-7)\) | |
| \((2;1)\) và \((-2;-7)\) | |
| \((-2;-7)\) |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
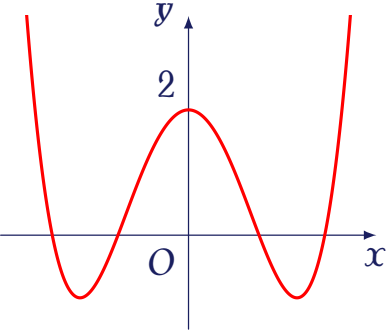
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Hàm số nào dưới đây có bảng biến thiên như sau?
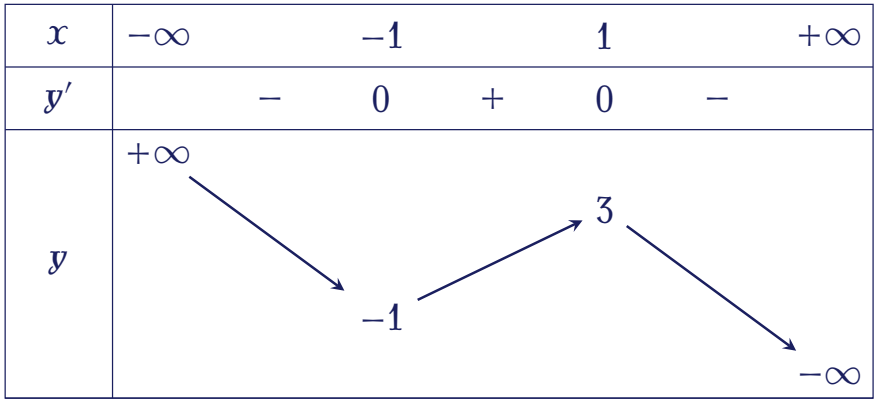
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
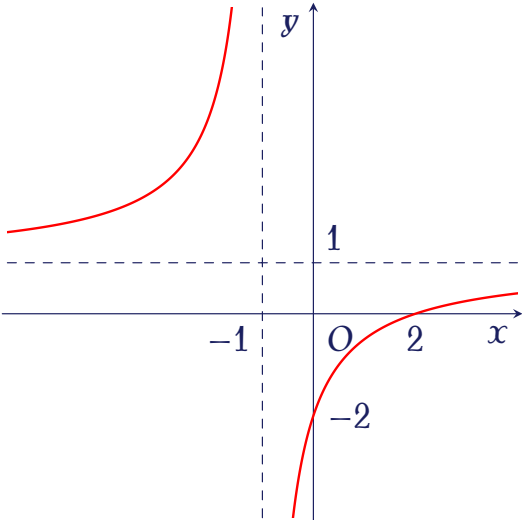
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
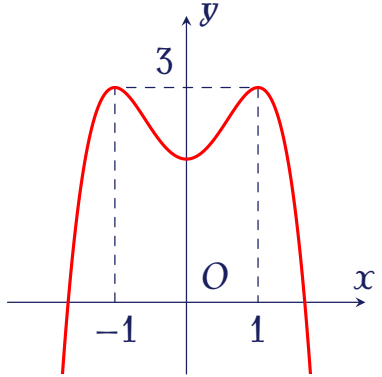
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
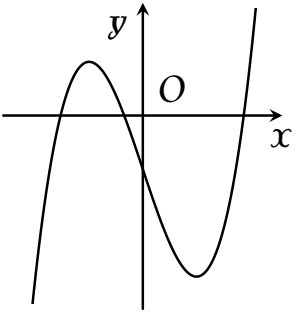
| $y=x^4-2x^2-1$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^3-3x-1$ | |
| $y=x^2+x-1$ |
Đồ thị của hàm số $y=x^3-3x+2$ cắt trục tung tại điểm có tung độ bằng
| $0$ | |
| $1$ | |
| $2$ | |
| $-2$ |
Đường thẳng nào sau đây tiếp xúc với parabol $\left(\mathscr{P}\right)\colon y=2x^2-5x+3$?
| $y=x+2$ | |
| $y=-x-1$ | |
| $y=x+3$ | |
| $y=-x+1$ |
Cho đồ thị \(\left(\mathscr{C}\right)\colon y=x^4-2x^2\). Đường thẳng nào sau đây cắt \(\left(\mathscr{C}\right)\) tại \(2\) điểm phân biệt?
| \(y=0\) | |
| \(y=1\) | |
| \(y=-\dfrac{3}{2}\) | |
| \(y=-\dfrac{1}{2}\) |
Đồ thị của hai hàm số \(y=-x^3+3x^2+2x-1\) và \(y=3x^2-2x-1\) có tất cả bao nhiêu điểm chung?
| \(1\) | |
| \(2\) | |
| \(0\) | |
| \(3\) |
Tìm tọa độ giao điểm \(M\) của đồ thị hàm số \(y=\dfrac{2x-1}{x+2}\) với trục tung.
| \(M\left(\dfrac{1}{2};0\right)\) | |
| \(M\left(0;2\right)\) | |
| \(M\left(0;-\dfrac{1}{2}\right)\) | |
| \(M\left(-\dfrac{1}{2};0\right)\) |
