Ngân hàng bài tập
B
Cho hình chóp $S.ABCD$ có các cặp cạnh đối không song song. Gọi $I$ là giao điểm $AB$ và $DC$. Đường thẳng $SI$ là giao tuyến của cặp mặt phẳng nào?
| $(SAD)$ và $(SBC)$ | |
| $(SAB)$ và $(SCD)$ | |
| $(SAD)$ và $(SCD)$ | |
| $(SAC)$ và $(SBD)$ |
1 lời giải
Chọn phương án B.
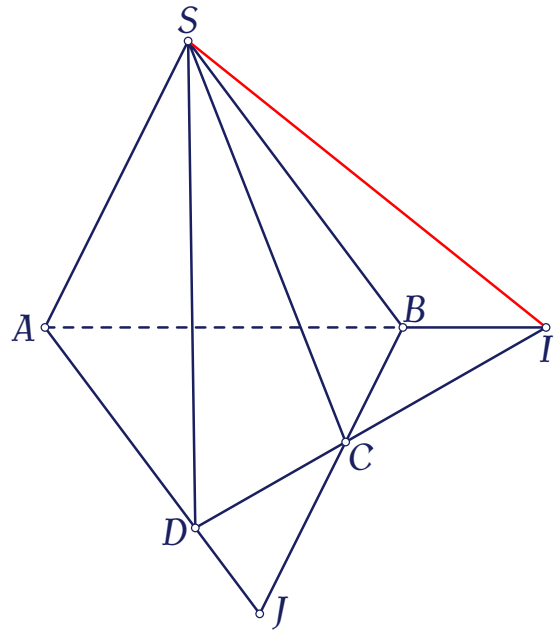
Vì $I$ là giao điểm $AB$ và $DC$ nên $I$ là điểm chung của hai mặt phẳng $(SAB)$ và $(SCD)$.
