Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=x^{2}+10x$, $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=f\left(x^4-8x^2+m\right)$ có đúng $9$ điểm cực trị?
| $16$ | |
| $9$ | |
| $15$ | |
| $10$ |
Chọn phương án D.
Cho $f'(x)=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=-10.\end{array}\right.$
Ta có $y'=\left(4x^3-16x\right)\cdot f'\left(x^4-8x^2+m\right)$.
$\begin{aligned}
\text{Cho }y'=0&\Leftrightarrow\left[\begin{array}{l}4x^3-16x=0\\ f'\left(x^4-8x^2+m\right)=0\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}
x=0,\,x=2,\,x=-2\\
x^4-8x^2+m=0\\
x^4-8x^2+m=-10
\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{ll}
x=0,\,x=2,\,x=-2\\
m=-x^4+8x^2 &(1)\\
m=-x^4+8x^2-10 &(2)
\end{array}\right.
\end{aligned}$
Ta cần tìm $m$ sao cho đường thẳng $y=m$ cắt các đồ thị $g(x)=-x^4+8x^2$ và $h(x)=-x^4+8x^2-10$ tại $6$ điểm phân biệt khác $0$ và $\pm2$ (*).
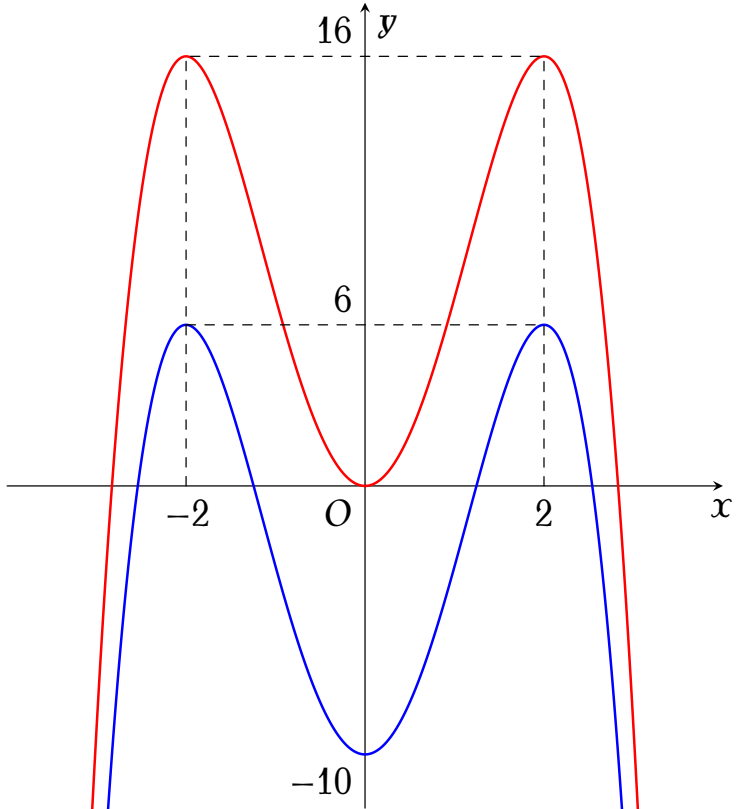
Từ đồ thị ta có các trường hợp sau:
- $-10<m<0$: Tổng số nghiệm của (1) và (2) là $6$ (thỏa (*))
- $m=0$: Tổng số nghiệm của (1) và (2) là $7$, trong đó có $x=0$ là nghiệm bội hai, vậy $y'=0$ có $9$ nghiệm, trong đó có $x=0$ là nghiệm bội ba (thỏa đề)
Vì $m$ nguyên nên $m\in\{-9;-8;\ldots;-1;0\}$, tức là có $10$ số nguyên $m$ thỏa đề.
