Có bao nhiêu số nguyên $a$ sao cho ứng với mỗi $a$, tồn tại ít nhất bốn số nguyên $b\in(-12;12)$ thỏa mãn $4^{a^2+b}\leq3^{b-a}+65$?
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
Chọn phương án D.
$\begin{aligned}
4^{a^2+b}\leq3^{b-a}+65&\Leftrightarrow4^{a^2}\cdot4^b\leq3^b\cdot3^{-a}+65\\
&\Leftrightarrow4^{a^2}\leq\left(\dfrac{3}{4}\right)^b\cdot3^{-a}+65\cdot\left(\dfrac{1}{4}\right)^b\\
&\Leftrightarrow\left(\dfrac{3}{4}\right)^b\cdot3^{-a}+65\cdot\left(\dfrac{1}{4}\right)^b-4^{a^2}\geq0\quad(1)
\end{aligned}$
Xét hàm số $f(b)=\left(\dfrac{3}{4}\right)^b\cdot3^{-a}+65\cdot\left(\dfrac{1}{4}\right)^b-4^{a^2}$ với $a$ là tham số.
Ta có $f'(b)=3^{-a}\left(\dfrac{3}{4}\right)^b\ln\left(\dfrac{3}{4}\right)+65\cdot\left(\dfrac{1}{4}\right)^b\ln\dfrac{1}{4}<0$ với $\forall b$.
Suy ra $f(b)$ nghịch biến trên $\mathbb{R}$.
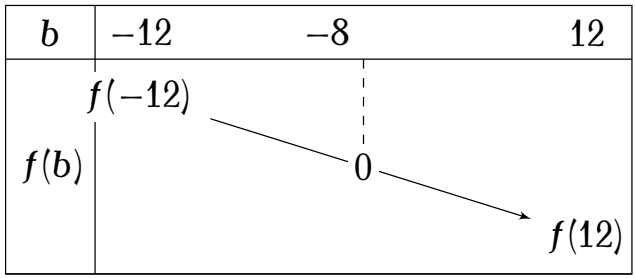
Để tồn tại ít nhất bốn số nguyên $b\in(-12;12)$ thỏa mãn bất phương trình (1) thì $f(-8)\geq0$, tức là $$\left(\dfrac{3}{4}\right)^{-8}\cdot3^{-a}+65\cdot\left(\dfrac{1}{4}\right)^{-8}-4^{a^2}\geq0\quad(2)$$
Xét hàm số $g(a)=\left(\dfrac{3}{4}\right)^{-8}\cdot3^{-a}+65\cdot\left(\dfrac{1}{4}\right)^{-8}-4^{a^2}$ ta có $$g'(a)=-\left(\dfrac{3}{4}\right)^{-8}\cdot3^{-a}\ln3-2a\cdot4^{a^2}\ln4$$
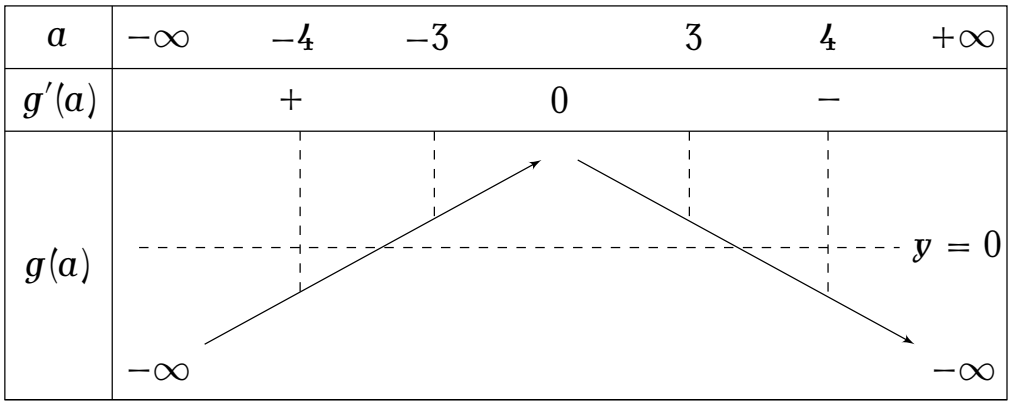
Dựa vào bảng biến thiên ta thấy (2) có $7$ nghiệm nguyên $a\in\{-3;-2;-1;0;1;2;3\}$.
