Ngân hàng bài tập
C
Cho hàm số $y=ax^4+bx^2+c$ ($a,\,b,\,c\in\mathbb{R})$ có đồ thị là đường cong trong hình bên.
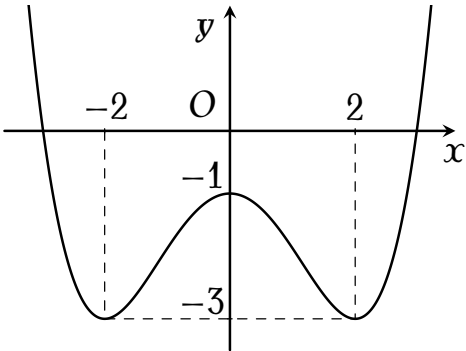
Giá trị cực đại của hàm số đã cho bằng
| $0$ | |
| $-1$ | |
| $-3$ | |
| $2$ |
1 lời giải
Chọn phương án B.
Dựa vào đồ thị ta thấy hàm số đạt cực đại tại điểm $x=0$, với giá trị cực đại là $-1$.
