Ngân hàng bài tập
B
Cho hàm số \(y=x+\sqrt{12-3x^2}\). Khẳng định nào sau đây đúng?
| Hàm số đạt cực đại tại \(x=-1\) | |
| Hàm số đạt cực đại tại \(x=1\) | |
| Hàm số đạt cực tiểu tại \(x=-1\) | |
| Hàm số đạt cực tiểu tại \(x=1\) |
1 lời giải
Chọn phương án B.
Điều kiện xác định: \(12-3x^2\geq0\Leftrightarrow x\in[-2;2]\).
Vậy tập xác định là \(\mathscr{D}=[-2;2]\).
Ta có \(y'=1-\dfrac{3x}{\sqrt{12-3x^2}}=\dfrac{\sqrt{12-3x^2}-3x}{\sqrt{12-3x^2}}\).$$\begin{aligned}
y'=0\Leftrightarrow&\sqrt{12-3x^2}-3x=0\\
\Leftrightarrow&\sqrt{12-3x^2}=3x\\
\Leftrightarrow&\begin{cases}
x\geq0\\
12-3x^2=9x^2
\end{cases}\\
\Leftrightarrow&\begin{cases}
x\geq0\\
12x^2-12=0
\end{cases}\\
\Leftrightarrow&\begin{cases}
x\geq0\\
\left[\begin{array}{ll}x=1 &\text{(nhận)}\\ x=-1 &\text{(loại)}\end{array}\right.
\end{cases}\\
\end{aligned}$$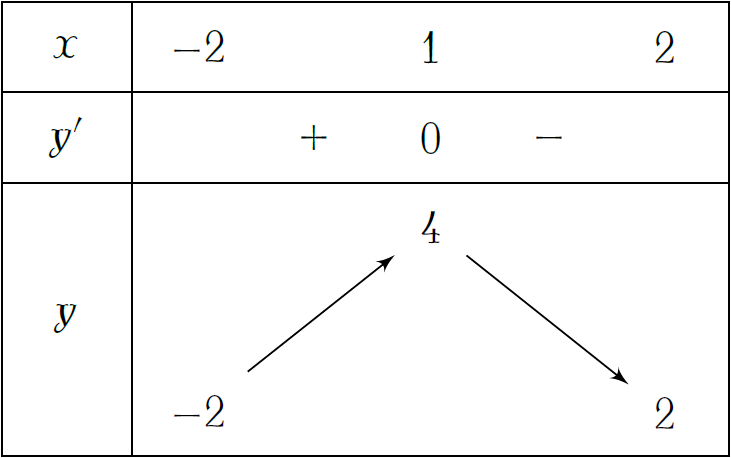
Vậy hàm số đạt cực đại tại \(x=1\).
