Cho phương trình \(x^2+y^2-2\left(m+1\right)x+4y-1=0\) (1). Với giá trị nào của \(m\) để (1) là phương trình đường tròn có bán kính nhỏ nhất?
| \(m=2\) | |
| \(m=-1\) | |
| \(m=1\) | |
| \(m=-2\) |
Chọn phương án B.
Ta có \(\begin{cases}
a=\dfrac{-2(m+1)}{-2}=m+1\\
b=\dfrac{4}{-2}=-2\\
c=-1.
\end{cases}\)
Đường tròn đã cho có bán kính là $$R=\sqrt{(m+1)^2+(-2)^2-(-1)}=\sqrt{(m+1)^2+5}$$
Dùng chức năng r trên máy tính cầm tay ta được:
- \(m=2\)
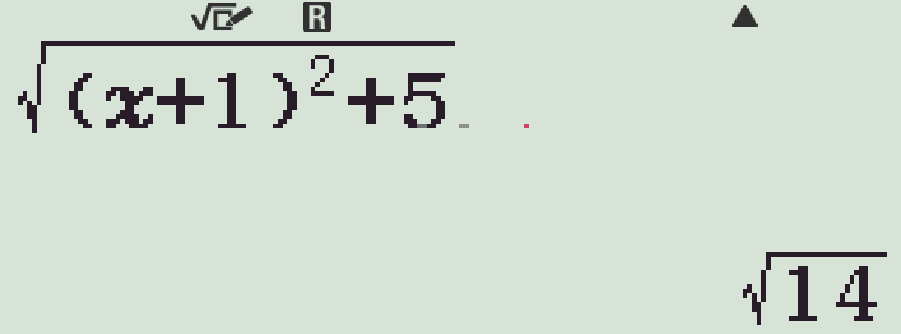
- \(m=-1\)
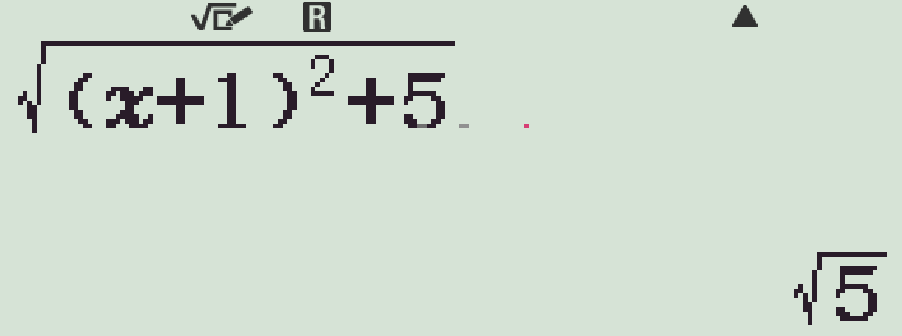
- \(m=1\)
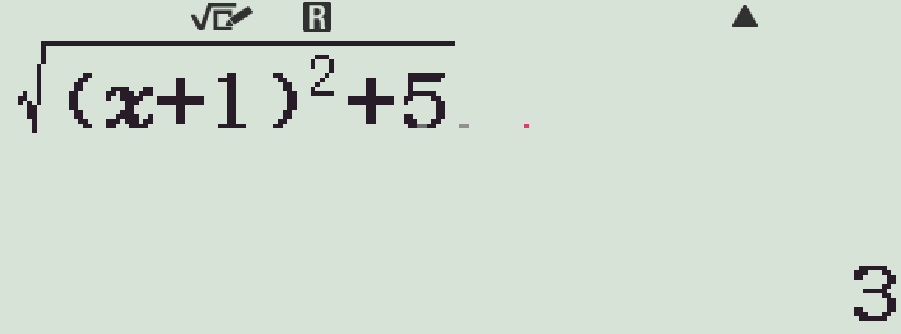
- \(m=-2\)
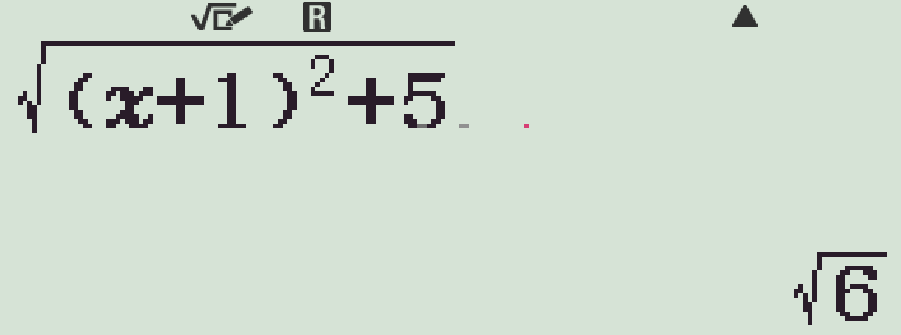
Vậy khi \(m=-1\) thì bán kính nhỏ nhất.
Chọn phương án B.
Ta có \(\begin{cases}
a=\dfrac{-2(m+1)}{-2}=m+1\\
b=\dfrac{4}{-2}=-2\\
c=-1.
\end{cases}\)
Để \(\left(1\right)\) là phương trình của đường tròn thì $$\begin{eqnarray*}
&a^2+b^2-c&>0\\
\Leftrightarrow&(m+1)^2+(-2)^2-(-1)&>0\\
\Leftrightarrow&(m+1)^2+5&>0\\
\end{eqnarray*}$$
Vì \((m+1)^2+5>0\) với \(\forall m\) nên \((1)\) luôn là phương trình đường tròn với bán kính \(R=\sqrt{(m+1)^2+5}\).
Để \(R\) nhỏ nhất thì \(m+1=0\Leftrightarrow m=-1\).
