Ngân hàng bài tập
B
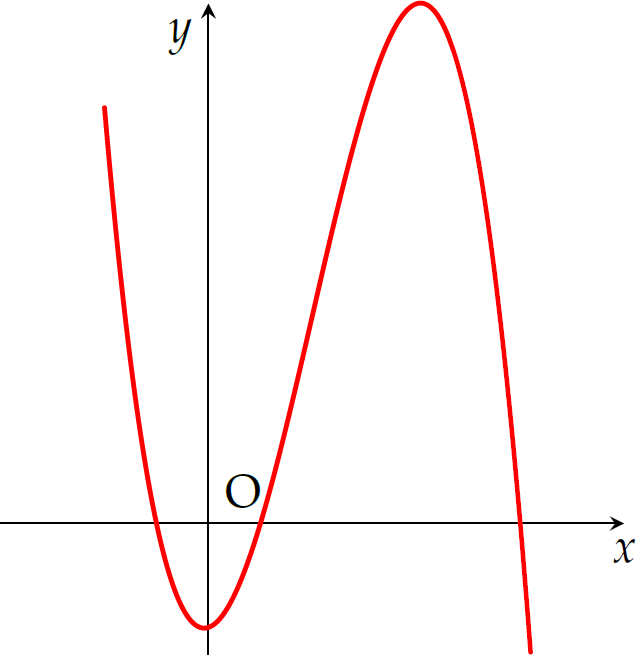
Đường cong ở hình trên là đồ thị của hàm số \(y=ax^3+bx^2+c\); với \(x\) là biến số thực; \(a,\,b,\,c\) là ba hằng số thực, \(a\neq0\). Mệnh đề nào dưới đây đúng?
| \(b<0< a\) và \(c<0\) | |
| \(a<0< b\) và \(c<0\) | |
| \(a< b<0\) và \(c<0\) | |
| \(a<0< b\) và \(c>0\) |
1 lời giải
Chọn phương án B.
- Quan sát sự biến thiên của hàm số ta thấy \(a<0\).
- Vì đồ thị cắt trục tung tại điểm nằm phía dưới trục hoành nên suy ra \(c<0\).
- \(y'=3ax^2+2bx=x(3a+2b)\).
Cho \(y'=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=-\dfrac{2b}{3a}\end{array}\right.\)
Từ hình vẽ ta thấy \(x=-\dfrac{2b}{3a}>0\) là điểm cực đại.
Lại vì \(a<0\) nên suy ra \(b>0\).
