Ngân hàng bài tập
SS
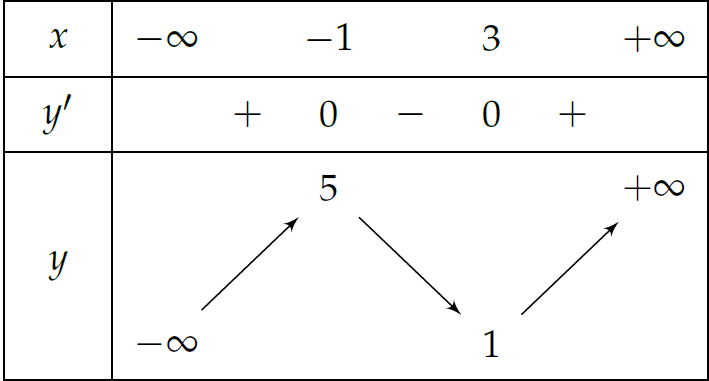
Cho hàm số \(y=f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình trên. Số điểm cực trị của hàm số \(y=\left|f(x-2)-3\right|\) bằng
| \(5\) | |
| \(4\) | |
| \(6\) | |
| \(3\) |
1 lời giải
Chọn phương án A.
Xét hàm số \(g(x)=f(x-2)-3\) ta có
- \(g(1)=f(1-2)-3=f(-1)-3=5-3=2\).
- \(g(5)=f(5-2)-3=f(3)-3=1-3=-2\).
Vậy hàm số \(g(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
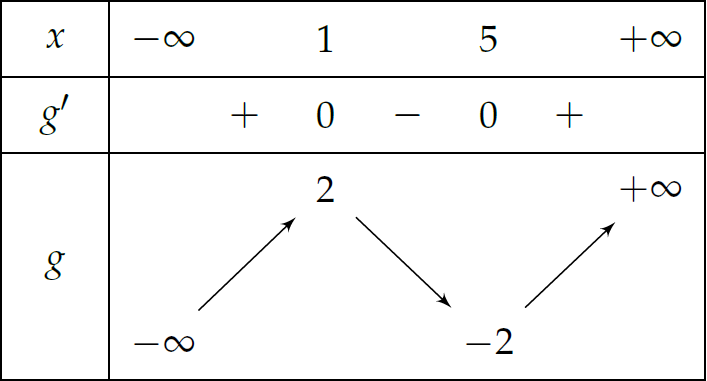
Vì \(\left|f(x-2)-3\right|=\left|g(x)\right|=\begin{cases}
g(x) &\text{khi }g(x)\geq0\\
-g(x) &\text{khi }g(x)<0
\end{cases}\) nên ta có bảng biến thiên sau:
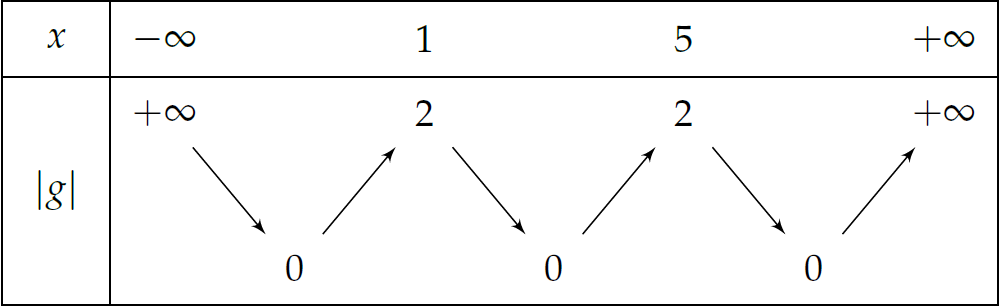
Vậy hàm số \(y=\left|f(x-2)-3\right|\) có \(5\) điểm cực trị.
