Cho $x,\,y$ là các số thực thỏa mãn $(x-3)^2+(y-1)^2=5$. Giá trị nhỏ nhất của biểu thức $P=\dfrac{3y^2+4xy+7x+4y-1}{x+2y+1}$ là
| $2\sqrt{3}$ | |
| $\dfrac{114}{11}$ | |
| $\sqrt{3}$ | |
| $3$ |
Chọn phương án D.
$\begin{aligned}
(x-3)^2+(y-1)^2=5&\Leftrightarrow x^2+y^2-6x-2y+5=0\\
&\Leftrightarrow6x+2y=x^2+y^2+5.
\end{aligned}$
Thay vào $P$ ta được $$\begin{aligned}
P&=\dfrac{3y^2+4xy+x+2y-1+(6x+2y)}{x+2y+1}\\
&=\dfrac{3y^2+4xy+x+2y-1+\big(x^2+y^2+5\big)}{x+2y+1}\\
&=\dfrac{x^2+4y^2+4xy+x+2y+4}{x+2y+1}\\
&=\dfrac{(x+2y+1)^2-(x+2y+1)+4}{x+2y+1}\\
&=(x+2y+1)-1+\dfrac{4}{x+2y+1}
\end{aligned}$$
Đặt $t=x+2y+1$, ta được $P=t-1+\dfrac{4}{t}$.
\begin{eqnarray*}
&\big[1\cdot(x-3)+2\cdot(y-1)\big]^2&\leq(1^2+2^2)\big[(x-3)^2+(y-1)\big]^2\\
\Leftrightarrow&[x+2y-5]^2&\leq25\\
\Leftrightarrow&-5&\leq x+2y-5\leq5\\
\Leftrightarrow&1&\leq x+2y+1\leq11\\
\Leftrightarrow&1&\leq t\leq11
\end{eqnarray*}
Xét hàm số $f(t)=t-1+\dfrac{4}{t}$ trên đoạn $[1;11]$.
Ta có $f'(t)=1-\dfrac{4}{t^2}$. Cho $f'(t)=0\Leftrightarrow\left[\begin{array}{ll}t=2 &\in[1;11]\\ t=-2 &\notin[1;11]\end{array}\right.$
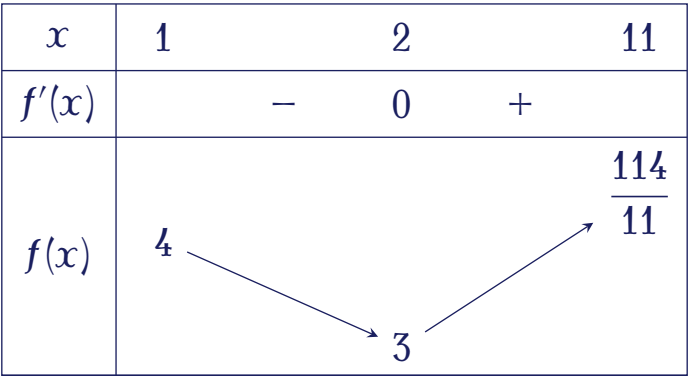
Vậy $\min\limits_{[1;11]}f(x)=3$. Suy ra giá trị nhỏ nhất của $P$ là $3$.
