Ngân hàng bài tập
B
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh $SA$.
| $2a\sqrt{3}$ | |
| $\sqrt{3}$ | |
| $2a$ | |
| $a$ |
1 lời giải
Chọn phương án D.
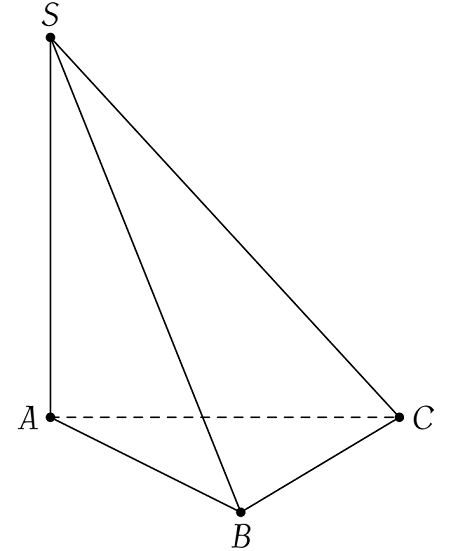
Ta có $V_{S.ABC}=\dfrac{1}{3}SA\cdot S_{\triangle ABC}$
$\Rightarrow SA=\dfrac{3V_{S.ABC}}{S_{\triangle ABC}}=\dfrac{3a^3\sqrt{3}}{\left(2a\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}}=a$.
