Ngân hàng bài tập
A
Tìm giá trị lớn nhất của hàm số $y=4x-\sqrt{2}x^2$.
| $\sqrt{2}$ | |
| $2\sqrt{2}$ | |
| $2$ | |
| $4$ |
1 lời giải
Chọn phương án B.
Hàm số bậc hai có $a=-\sqrt{2}<0$ nên đồ thị là một parabol úp xuống, điểm cao nhất của đồ thị là đỉnh $I\left(\sqrt{2};2\sqrt{2}\right)$.
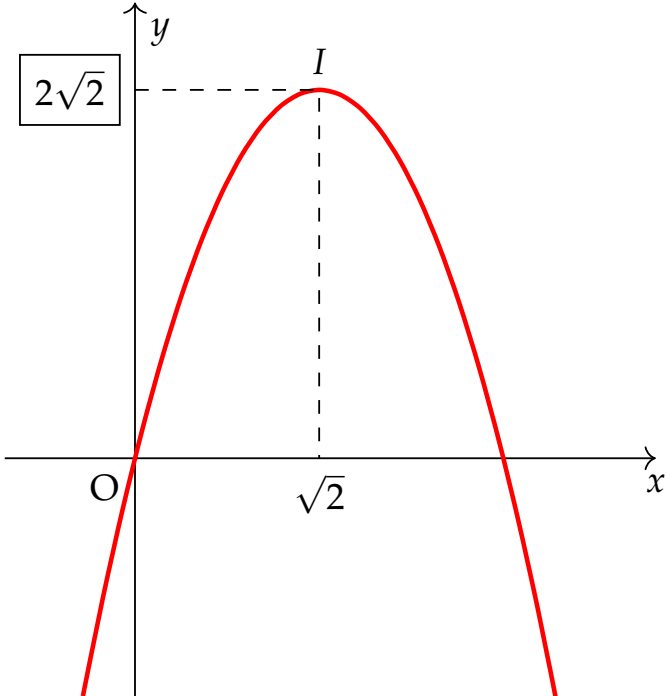
Vậy hàm số có giá trị lớn nhất là $2\sqrt{2}$.
