Ngân hàng bài tập
C
Tìm giá trị nhỏ nhất của hàm số \(y=x+1+\dfrac{4}{x}\) trên đoạn \([1;3]\).
| \(4\) | |
| \(\dfrac{16}{3}\) | |
| \(5\) | |
| \(6\) |
1 lời giải
Chọn phương án C.
Ta có \(y'=1-\dfrac{4}{x^2}=\dfrac{x^2-4}{x^2}\).
Cho \(y'=0\Leftrightarrow x^2-4=0\Leftrightarrow\left[\begin{array}{ll}x=2 &\in[1;3]\\ x=-2 &\notin[1;3]\end{array}\right.\)
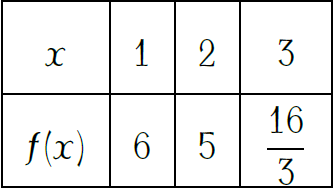
Vậy \(\min\limits_{[1;3]}f(x)=5\).
