Ngân hàng bài tập
A
Tìm điểm cực đại của đồ thị hàm số $$y=\dfrac{x}{2}+\dfrac{2}{x}$$
| \(N(-2;-2)\) | |
| \(x=-2\) | |
| \(M(2;2)\) | |
| \(x=2\) |
1 lời giải
Chọn phương án A.
Tập xác định: \(\mathscr{D}=\mathbb{R}\setminus\{0\}\).
Ta có \(y'=\dfrac{1}{2}-\dfrac{2}{x^2}=\dfrac{x^2-4}{2x^2}\).
Cho \(y'=0\Leftrightarrow x^2-4=0\Leftrightarrow\left[\begin{array}{l}x=2\\ x=-2\end{array}\right.\)
Bảng biến thiên: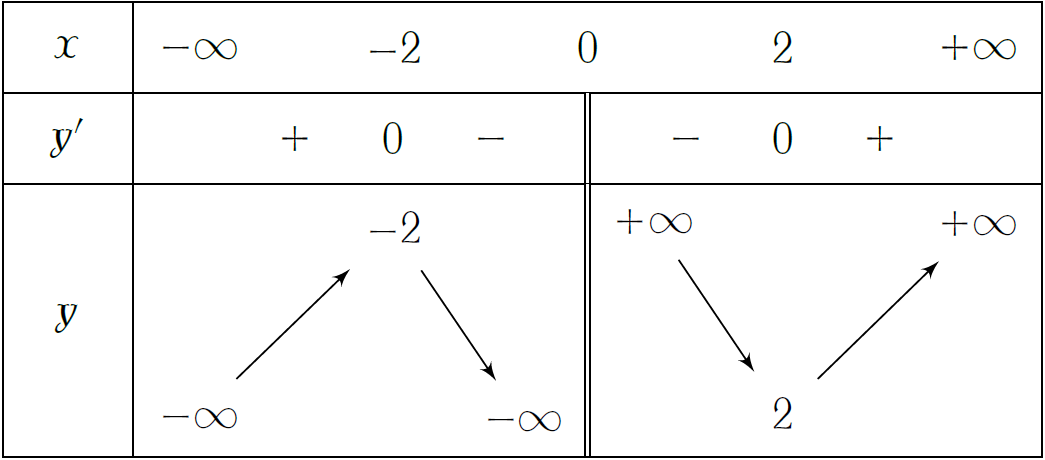
Vậy điểm cực đại của đồ thị hàm số \(y=\dfrac{x}{2}+\dfrac{2}{x}\) là \(N(-2;-2)\).
