Ngân hàng bài tập
A
Tìm tập nghiệm \(S\) của bất phương trình \(x^2-4x+4>0\).
| \(S=\Bbb{R}\setminus\{2\}\) | |
| \(S=\Bbb{R}\) | |
| \(S=(2;+\infty)\) | |
| \(S=\Bbb{R}\setminus\{-2\}\) |
2 lời giải
Chọn phương án A.
Ta thấy \(x^2-4x+4=(x-2)^2\geq0\), \(\forall x\in\Bbb{R}\).
Và \(x^2-4x+4=0\Leftrightarrow x=2\).
Do đó \(x^2-4x+4>0\Leftrightarrow x\neq2\).
Suy ra \(S=\Bbb{R}\setminus\{2\}\).
Chọn phương án A.
Bảng xét dấu: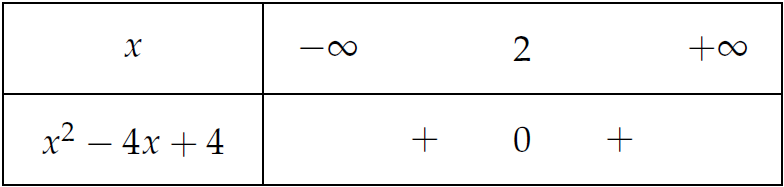
Vậy \(S=(-\infty;2)\cup(2;+\infty)=\Bbb{R}\setminus\{2\}\).
