Ngân hàng bài tập
B
Tam thức bậc hai \(f(x)=x^2-4x-5\) nhận giá trị âm trên khoảng nào sau đây?
| \((5;1)\) | |
| \((-5;-1)\) | |
| \((-5;1)\) | |
| \((-1;5)\) |
2 lời giải
Chọn phương án D.
Ta có thể dùng chức năng TABLE trên máy tính cầm tay để tìm ra khoảng âm của \(f(x)\).
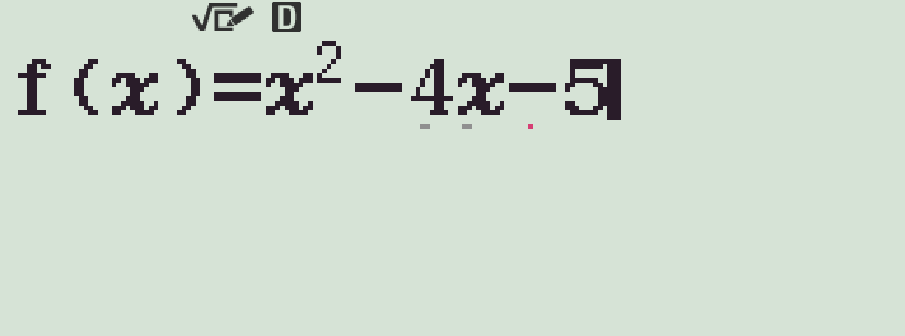
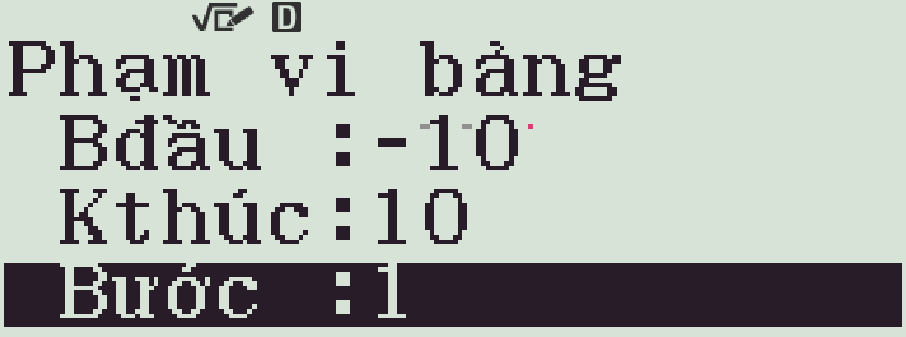
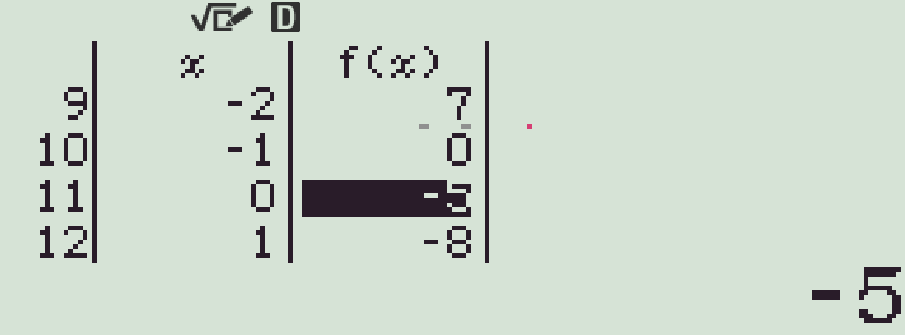
Từ đó ta thấy \(f(x)<0\) trên khoảng \((-1;5)\).
Chọn phương án D.
Bảng xét dấu: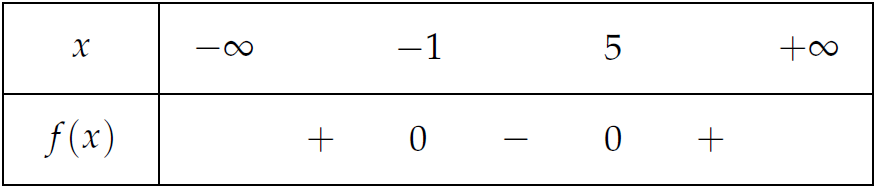
Vậy \(f(x)<0\Leftrightarrow x\in(-1;5)\).
