Ngân hàng bài tập
B
Tam thức bậc hai \(f(x)=-x^2+3x-2\) nhận giá trị không âm khi và chỉ khi
| \(x\in(-\infty;1)\cup(2;+\infty)\) | |
| \(x\in[1;2]\) | |
| \(x\in(-\infty;1]\cup[2;+\infty)\) | |
| \(x\in(1;2)\) |
1 lời giải
Chọn phương án B.
\(-x^2+3x-2=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=2.\end{array}\right.\)
Bảng xét dấu: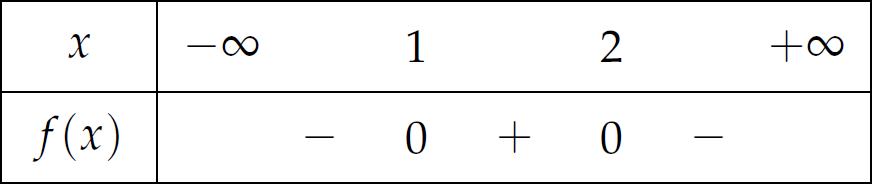
Theo đó, \(f(x)\geq0\Leftrightarrow x\in[1;2]\).
