Ngân hàng bài tập
B
Tìm số phức liên hợp của số phức \(z\), biết rằng $$4z+(2+3\mathrm{i})(1-2\mathrm{i})=4+3\mathrm{i}$$
| \(\overline{z}=-1-\dfrac{5}{4}\mathrm{i}\) | |
| \(\overline{z}=1-\dfrac{5}{4}\mathrm{i}\) | |
| \(\overline{z}=-1+\dfrac{5}{4}\mathrm{i}\) | |
| \(\overline{z}=-1-\mathrm{i}\) |
2 lời giải
Chọn phương án D.
Dùng máy tính cầm tay:
- Nhập \(4+3\mathrm{i}-(2+3\mathrm{i})(1-2\mathrm{i})\)=
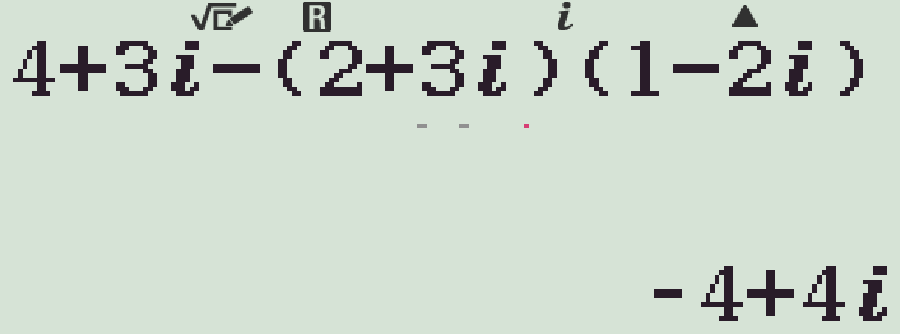
- Nhập T2aMR4)=
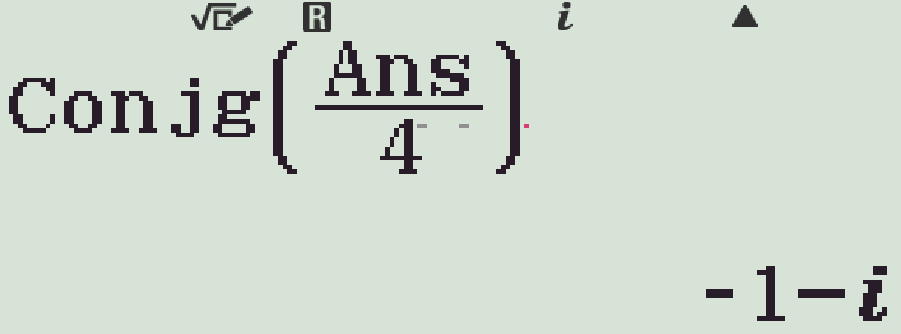
Chọn phương án D.
Ta có \(4z=4+3\mathrm{i}-(2+3\mathrm{i})(1-2\mathrm{i})=-4+4\mathrm{i}\).
Suy ra \(z=-1+\mathrm{i}\).
Vậy \(\overline{z}=-1-\mathrm{i}\).
