Ngân hàng bài tập
C
Cho số phức \(z=2+3\mathrm{i}\). Tính \(\dfrac{z}{\overline{z}}\).
| \(\dfrac{-5+12\mathrm{i}}{13}\) | |
| \(\dfrac{5-6\mathrm{i}}{11}\) | |
| \(\dfrac{5-12\mathrm{i}}{13}\) | |
| \(\dfrac{-5-12\mathrm{i}}{13}\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Nhập \(2+3\mathrm{i}\)=

- Nhập aMRT2M)=
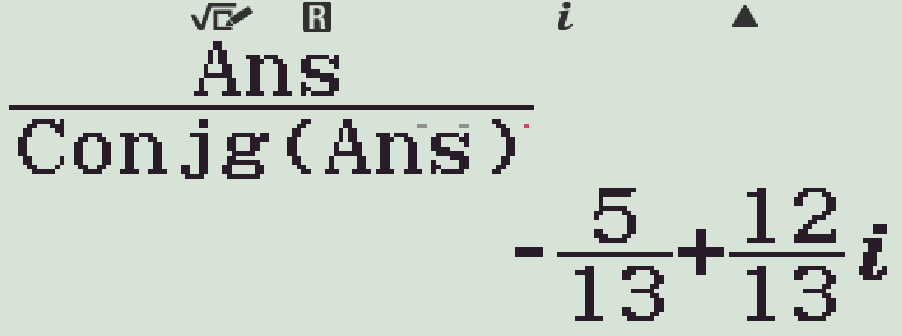
Chọn phương án A.
\(\begin{aligned}
\dfrac{z}{\overline{z}}&=\dfrac{z\cdot z}{\overline{z}\cdot z}=\dfrac{z^2}{|z|^2}\\
&=\dfrac{(2+3\mathrm{i})^2}{2^2+3^2}=\dfrac{-5+12\mathrm{i}}{13}.
\end{aligned}\)
