Ngân hàng bài tập
B
Cho số phức \(z=1-\dfrac{1}{3}\mathrm{i}\). Tìm số phức \(w=\mathrm{i}\overline{z}+3z\).
| \(w=\dfrac{8}{3}\) | |
| \(w=\dfrac{8}{3}+\mathrm{i}\) | |
| \(w=\dfrac{10}{3}+\mathrm{i}\) | |
| \(w=\dfrac{10}{3}\) |
2 lời giải
Chọn phương án A.
Dùng máy tính cầm tay:
- Nhập \(1-\dfrac{1}{3}\mathrm{i}\)=

- Nhập bOT2M)+3M=
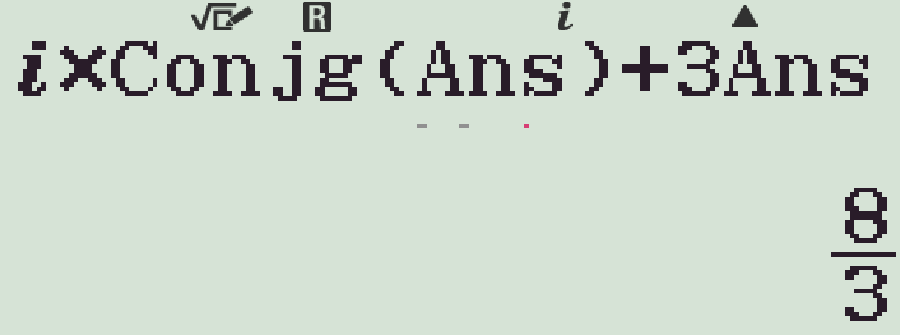
Chọn phương án A.
\(\begin{aligned}
w&=\mathrm{i}\left(1+\dfrac{1}{3}\mathrm{i}\right)+3\left(1-\dfrac{1}{3}\mathrm{i}\right)\\
&=\mathrm{i}-\dfrac{1}{3}+3-\mathrm{i}\\
&=\dfrac{8}{3}.
\end{aligned}\)
