Ngân hàng bài tập
A
Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x^2-2x,\;\forall x\in\mathbb{R}\). Hàm số \(y=-2f(x)\) đồng biến trên khoảng
| \((0;2)\) | |
| \((2;+\infty)\) | |
| \((-\infty;-2)\) | |
| \((-2;0)\) |
1 lời giải
Chọn phương án A.
Ta có \(y'=-2f'(x)=-2x^2+4x\).
Bảng biến thiên: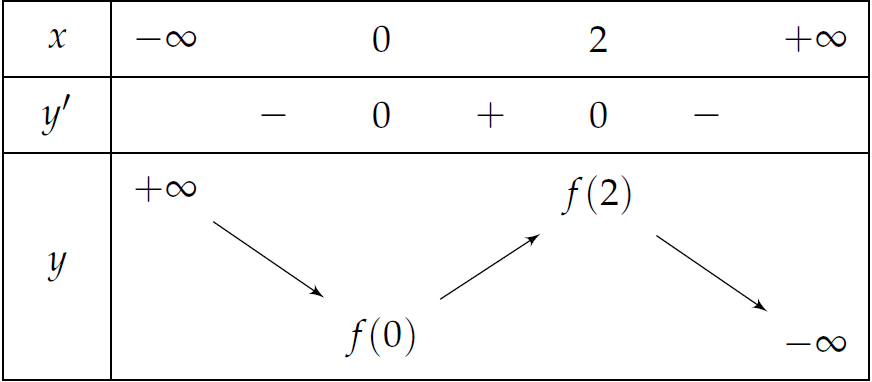
Vậy hàm số \(y=-2f(x)\) đồng biến trên khoảng \((0;2)\).
