Nếu \(\tan x=-3\) thì

	\(\cot x=-\dfrac{1}{3}\)
	\(\cot x=\dfrac{1}{3}\)
	\(\cos x=-\dfrac{1}{10}\)
	\(\cos x=\dfrac{1}{10}\)

Hãy chọn mệnh đề không đúng trong các mệnh đề sau đây:

	\(-1\leq\sin x\leq1\)
	\(\tan^2x\cdot\cot^2x=1\)
	\(-1\leq\cot x\leq1\)
	\(\sin^2x+\cos^2x=1\)

Cho cung \(\alpha\), với \(\pi<\alpha<\dfrac{3\pi}{2}\). Hãy chọn phát biểu đúng.

	\(\cos\alpha>0\)
	\(\tan\alpha<0\)
	\(\cot\alpha>0\)
	\(\sin\alpha>0\)

Trong đường tròn lượng giác, trục tung nhận giá trị nào của cung lượng giác?

	\(\cot\)
	\(\cos\)
	\(\tan\)
	\(\sin\)

Bánh xe đạp của bạn Trâm có bán kính \(40\) cm, bình thường tốc độ đạp của Trâm là \(3\) vòng/giây. Vậy mỗi giây Trâm đi được quãng đường bao nhiêu?

	\(377\) cm
	\(40\) cm
	\(120\) cm
	\(754\) cm

Trên đường tròn bán kính \(R\), cung \(\alpha=\dfrac{\pi}{10}\) có độ dài \(2\pi\) cm. Bán kính \(R\) bằng

	\(10\) cm
	\(\dfrac{20}{\pi^2}\) cm
	\(20\) cm
	\(\dfrac{\pi^2}{5}\) cm

Trên đường tròn bán kính \(12\) cm thì cung có số đo \(120^{\circ}\) có độ dài là

	\(8\pi\) cm
	\(8\pi\) m
	\(1440\) cm
	\(4\pi\) cm

Cung có số đo \(-\dfrac{7\pi}{2}\) thì có số đo độ là

	\(-630^{\circ}\)
	\(-0,19^{\circ}\)
	\(0,19\)
	\(630^{\circ}\)

Cung có số đo \(45^{\circ}\) thì số đo radian là

	\(\dfrac{\pi}{4}\)
	\(\dfrac{\pi}{2}\)
	\(\dfrac{\pi}{6}\)
	\(\dfrac{\pi}{3}\)

Cung có số đo \(x\) (rad) thì có số đo độ là

	\(\dfrac{x\pi}{180}\)
	\(\dfrac{\pi}{180x}\)
	\(\dfrac{180}{x\pi}\)
	\(\dfrac{180x}{\pi}\)

Hình nào dưới đây biểu diễn cung lượng giác \(400^\circ\)?

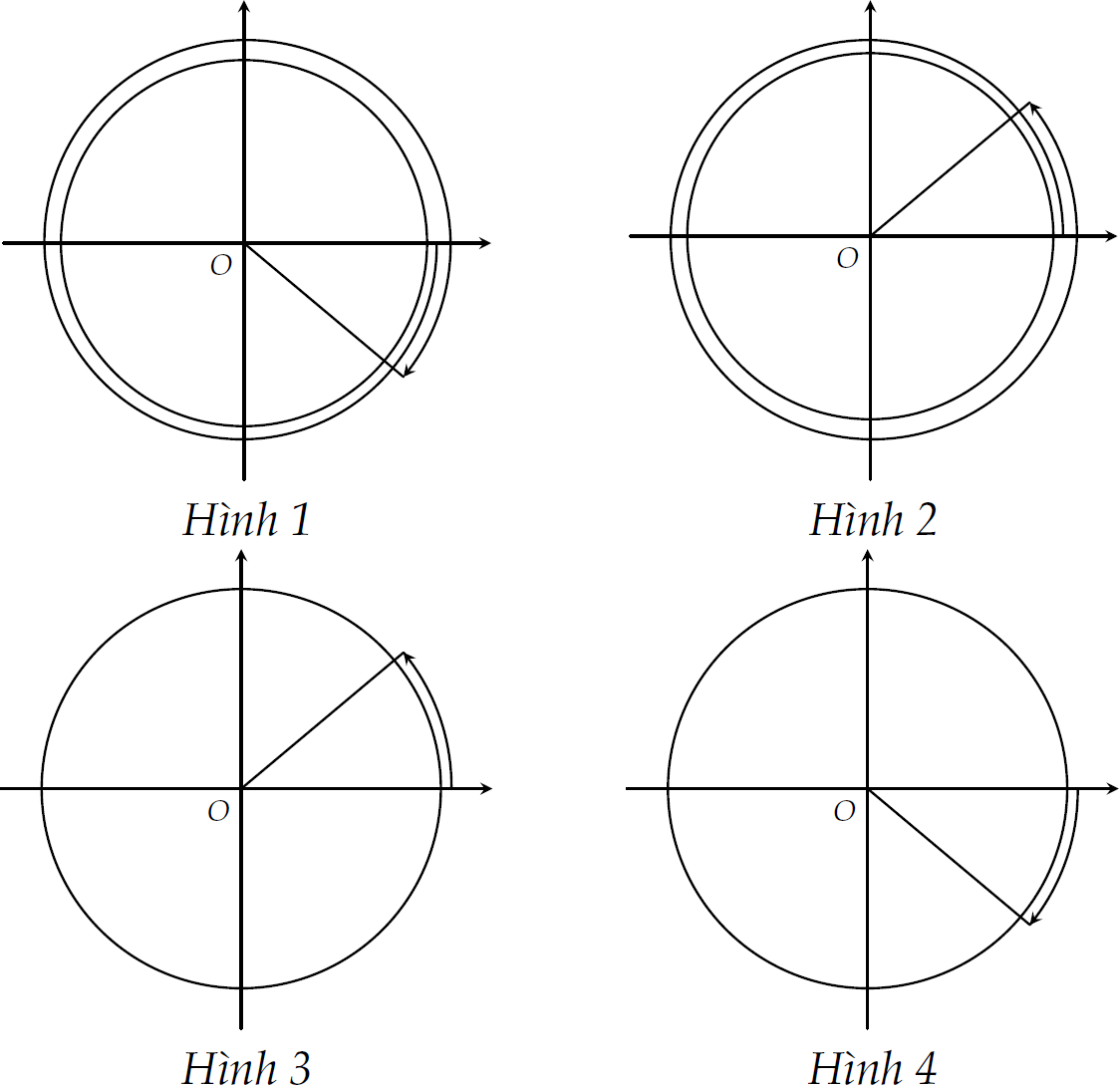
	Hình 1
	Hình 3
	Hình 4
	Hình 2

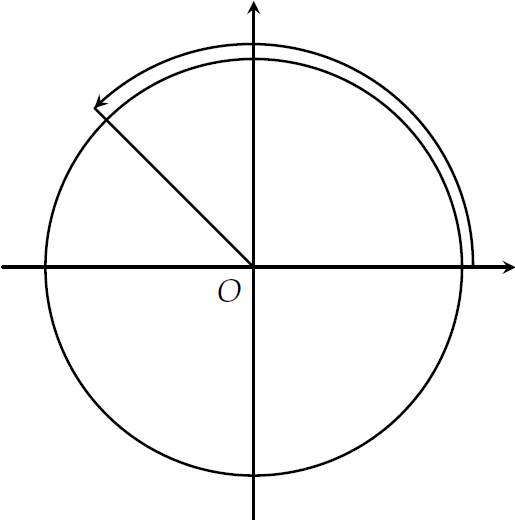
Hình trên mô tả cung tròn có số đo

	\(45^\circ\)
	\(135^\circ\)
	\(120^\circ\)
	\(150^\circ\)

Phát biểu nào sau đây không đúng về đường tròn lượng giác:

	Tâm \(O(0;0)\)
	Là đường tròn định hướng
	Có đường kính bằng \(1\)
	Có bán kính bằng \(1\)

Rút gọn biểu thức \(P=\dfrac{1+\sin^2x}{1-\sin^2x}\).

	\(P=1+2\tan^2x\)
	\(P=1-2\tan^2x\)
	\(P=2\tan^2x-1\)
	\(P=-1-2\tan^2x\)

Rút gọn biểu thức $$P=\sqrt{\sin^4x+\sin^2x\cos^2x}$$

	\(P=\left|\sin x\right|\)
	\(P=\sin x\)
	\(P=\cos x\)
	\(P=\left|\cos x\right|\)

Rút gọn biểu thức \(M=\cot^2x-\cos^2x\).

	\(M=\cot^2x\)
	\(M=\cos^2x\)
	\(M=1\)
	\(M=\cot^2x\cdot\cos^2x\)

Rút gọn biểu thức \(M=\tan^2x-\sin^2x\).

	\(M=\tan^2x\)
	\(M=\sin^2x\)
	\(M=\tan^2x\cdot\sin^2x\)
	\(M=1\)

Mệnh đề nào sau đây là đúng?

	\(\sin^4x-\cos^4x=1-2\cos^2x\)
	\(\sin^4x-\cos^4x=1-2\sin^2x\cos^2x\)
	\(\sin^4x-\cos^4x=1-2\sin^2x\)
	\(\sin^4x-\cos^4x=2\cos^2x-1\)

Tính giá trị của \(\cot\dfrac{89\pi}{6}\).

	\(\cot\dfrac{89\pi}{6}=\sqrt{3}\)
	\(\cot\dfrac{89\pi}{6}=-\sqrt{3}\)
	\(\cot\dfrac{89\pi}{6}=\dfrac{\sqrt{3}}{3}\)
	\(\cot\dfrac{89\pi}{6}=-\dfrac{\sqrt{3}}{3}\)

Tính giá trị của \(\sin\dfrac{47\pi}{6}\).

	\(\sin\dfrac{47\pi}{6}=\dfrac{\sqrt{3}}{2}\)
	\(\sin\dfrac{47\pi}{6}=\dfrac{1}{2}\)
	\(\sin\dfrac{47\pi}{6}=\dfrac{\sqrt{2}}{2}\)
	\(\sin\dfrac{47\pi}{6}=-\dfrac{1}{2}\)