Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x+2)^2(x-1)^5\big(x^2-2(m-6)x+m\big)$ với mọi $x\in\mathbb{R}$. Số giá trị nguyên dương của tham số $m$ để hàm số đã cho có đúng một điểm cực trị là
| $7$ | |
| $5$ | |
| $6$ | |
| $4$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
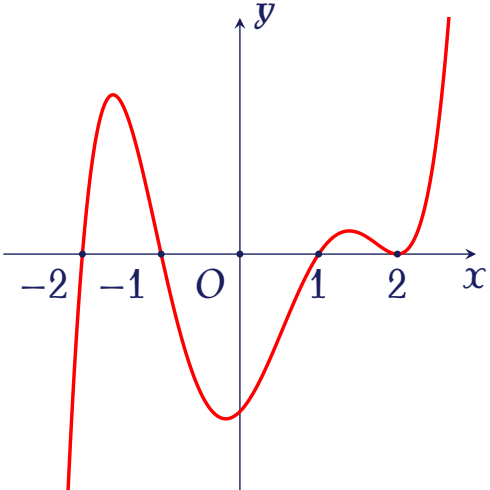
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=x^{2}+10x$, $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=f\left(x^4-8x^2+m\right)$ có đúng $9$ điểm cực trị?
| $16$ | |
| $9$ | |
| $15$ | |
| $10$ |
Tập hợp các giá trị của tham số \(m\) để hàm số \(y=\dfrac{x^3}{3}-6x^2+(m-2)x+11\) có \(2\) điểm cực trị trái dấu.
| \((-\infty;38)\) | |
| \((-\infty;2)\) | |
| \((-\infty;2]\) | |
| \((2;38)\) |
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=x^3-3x^2+mx+1\) có \(2\) điểm cực trị.
| \(m\leq3\) | |
| \(m>3\) | |
| \(m>-3\) | |
| \(m<3\) |
Tìm tất cả giá trị của tham số \(m\) để đồ thị hàm số \(y=x^4+(6m-4)x^2+1-m\) có \(3\) điểm cực trị.
| \(m\geq\dfrac{2}{3}\) | |
| \(m\leq\dfrac{2}{3}\) | |
| \(m>\dfrac{2}{3}\) | |
| \(m<\dfrac{2}{3}\) |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\big\{0;1\big\}$ | |
| $\big\{1\big\}$ | |
| $\big\{-1;1\big\}$ | |
| $\big\{0\big\}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=(m+2)x^4+(m-3)x^2+2022$ có ba cực trị là
| $4$ | |
| $2$ | |
| $3$ | |
| $6$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\big|3x^4-4x^3-12x^2+m\big|$ có $7$ điểm cực trị?
| $4$ | |
| $6$ | |
| $3$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y=-x^3+3x^2-3mx+\dfrac{5}{3}$ có đúng một cực trị thuộc khoảng $(-2;5)$?
| $16$ | |
| $6$ | |
| $17$ | |
| $7$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f'(x)=(x-1)^2(3-x)\big(x^2-x-1\big)$. Hỏi hàm số $f(x)$ có bao nhiêu điểm cực tiểu?
| $3$ | |
| $2$ | |
| $1$ | |
| $0$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $y=f(x)$ có đạo hàm $y=f'(x)$ với đồ thị như hình vẽ.
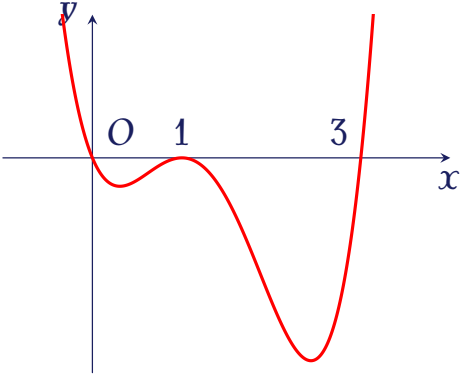
Tìm $m$ để hàm số $g(x)=f\big(x^2+m\big)$ có $3$ điểm cực trị.
| $m\in(-\infty;0]$ | |
| $m\in(3;+\infty)$ | |
| $m\in[0;3)$ | |
| $m\in(0;3)$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-1)^2\big(x^2-2x\big)$ với $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $f\big(x^2-8x+m\big)$ có $5$ điểm cực trị?
| $17$ | |
| $15$ | |
| $16$ | |
| $18$ |
Cho hàm số $y=f(x)$ có đạo hàm $y=f'(x)$ với đồ thị như hình vẽ.
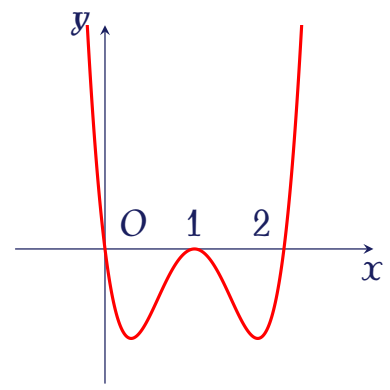
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g(x)=f\big(x^2-8x+m\big)$ có $5$ điểm cực trị.
| $15$ | |
| $16$ | |
| $17$ | |
| $18$ |
Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
