Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $BC=2a$ và $AA'=3a$ (tham khảo hình bên).
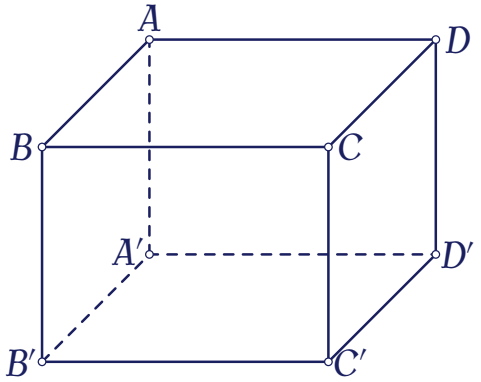
Khoảng cách giữa hai đường thẳng $BD$ và $A'C'$ bằng
| $a$ | |
| $a\sqrt{2}$ | |
| $2a$ | |
| $3a$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
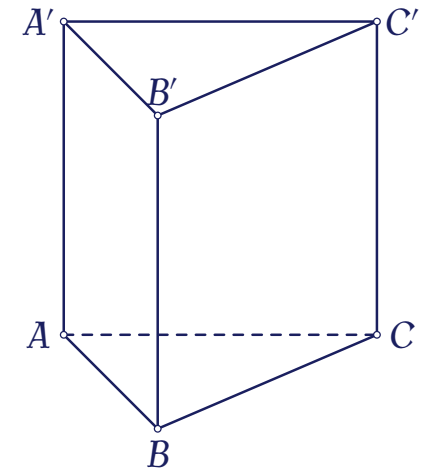
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
Cho lăng trụ đứng $ABC.A'B'C'$ có tất cả các cạnh bằng nhau và bằng $a$ (tham khảo hình bên).
Khoảng cách từ điểm $A$ đến mặt phẳng $(BCC'B')$ bằng
| $\dfrac{a\sqrt{3}}{4}$ | |
| $a$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ |
Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình vuông cạnh $a$, $SA\perp\left(ABCD\right)$ và $SA=a$.
Góc giữa hai đường thẳng $SD$ và $BC$ bằng
| $60^{\circ}$ | |
| $45^{\circ}$ | |
| $90^{\circ}$ | |
| $30^{\circ}$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng $AA'$ và $BC'$ bằng
| $30^\circ$ | |
| $90^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B$, $AB=2a$ và $SA$ vuông góc với mặt phẳng đáy. Khoảng cách từ $C$ đến mặt phẳng $(SAB)$ bằng
| $\sqrt2a$ | |
| $2a$ | |
| $a$ | |
| $2\sqrt2a$ |
Cho tứ diện $OABC$ có $OA,\,OB,\,OC$ đôi một vuông góc với nhau và $OA=OB=OC=a$. Gọi $D$ là trung điểm của đoạn $BC$. Khoảng cách giữa hai đường thẳng $OD$ và $AB$ bằng
| $\dfrac{a\sqrt{3}}{3}$ | |
| $\dfrac{a\sqrt{6}}{2}$ | |
| $\dfrac{a\sqrt{6}}{3}$ | |
| $\dfrac{a\sqrt{3}}{2}$ |
Cho hình chóp $S.ABCD$ có $SA$ vuông góc với mặt phẳng $\left(ABCD\right)$, $SA=a\sqrt{5}$, tứ giác $ABCD$ là hình chữ nhật, $AB=a$, $AD=2a$. Góc giữa đường thẳng $SC$ và mặt phẳng $\left(ABCD\right)$ bằng
| $45^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ | |
| $90^\circ$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$ và $AB=4$ (tham khảo hình bên).
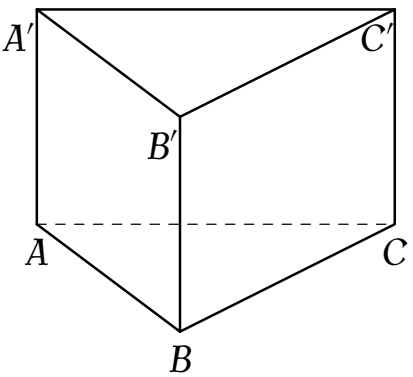
Khoảng cách từ $C$ đến mặt phẳng $\left(ABB'A'\right)$ bằng
| $2\sqrt{2}$ | |
| $2$ | |
| $\sqrt{2}$ | |
| $4$ |
Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
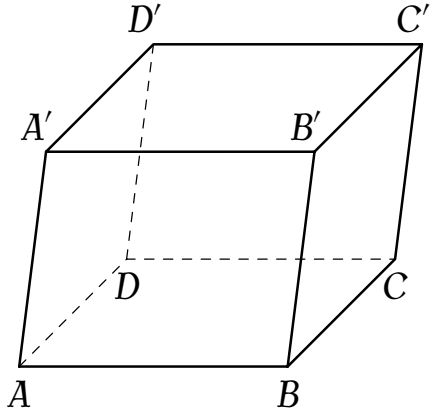
Góc giữa hai đường thẳng $A'C'$ và $BD$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $a$, góc giữa cạnh bên và mặt phẳng đáy bằng $60^\circ$. Tính độ dài đường cao của hình chóp đã cho.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $SA\bot (ABCD)$, $AB=a$ và $SB=\sqrt{2}a$. Khoảng cách từ điểm $S$ đến mặt phẳng $(ABCD)$ bằng
| $a$ | |
| $\sqrt{2}a$ | |
| $2a$ | |
| $\sqrt{3}a$ |
Cho hình chóp $S.ABCD$ có $SA$ vuông góc với mặt phẳng đáy. Mặt phẳng $\left(ABCD\right)$ vuông góc với mặt phẳng nào dưới đây?
| $(SAC)$ | |
| $(SBD)$ | |
| $(SCD)$ | |
| $(SBC)$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA\bot (ABCD)$ và $SA=a$. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABCD)$ bằng
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABCD$ có $ABCD$ là hình chữ nhật và $SA\bot (ABCD)$. Mệnh đề nào dưới đây đúng?
| $AB\bot(SAD)$ | |
| $BC\bot(SAD)$ | |
| $AC\bot(SAD)$ | |
| $BD\bot(SAD)$ |
Trong không gian cho hai vectơ $\overrightarrow{u}$, $\overrightarrow{v}$ tạo với nhau một góc $60^\circ$, $\left|\overrightarrow{u}\right|=2$ và $\left|\overrightarrow{v}\right|=3$. Tích vô hướng $\overrightarrow{u}\cdot\overrightarrow{v}$ bằng
| $3$ | |
| $6$ | |
| $2$ | |
| $3\sqrt{3}$ |
Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $a$. Khoảng cách từ $A'$ đến mặt phẳng $(ABCD)$ bằng
| $a$ | |
| $2a$ | |
| $3a$ | |
| $\dfrac{a}{2}$ |
Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật?
| $3$ | |
| $1$ | |
| $5$ | |
| $2$ |
Trong không gian cho điểm $A$ và mặt phẳng $(P)$. Mệnh đề nào dưới đây đúng?
| Có đúng một đường thẳng đi qua $A$ và vuông góc với $(P)$ | |
| Có đúng hai đường thẳng đi qua $A$ và vuông góc với $(P)$ | |
| Có vô số đường thẳng đi qua $A$ và vuông góc với $(P)$ | |
| Không tồn tại đường thẳng đi qua $A$ và vuông góc với $(P)$ |
Trong không gian, với $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ là ba vectơ bất kỳ, mệnh đề nào dưới đây đúng?
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}-\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{b}\cdot \overrightarrow{c}$ |
