Điểm nào sau đây không thuộc đồ thị hàm số $y=x^4-2x^2-1$?
| $A(-1;2)$ | |
| $B(2;7)$ | |
| $C(0;-1)$ | |
| $D(1;-2)$ |
Giá trị cực tiểu của hàm số $y=x^4-4x^2+3$ là
| $y_{\text{CT}}=0$ | |
| $y_{\text{CT}}=3$ | |
| $y_{\text{CT}}=\sqrt{2}$ | |
| $y_{\text{CT}}=-1$ |
Hàm số nào dưới đây có bảng biến thiên như hình bên?
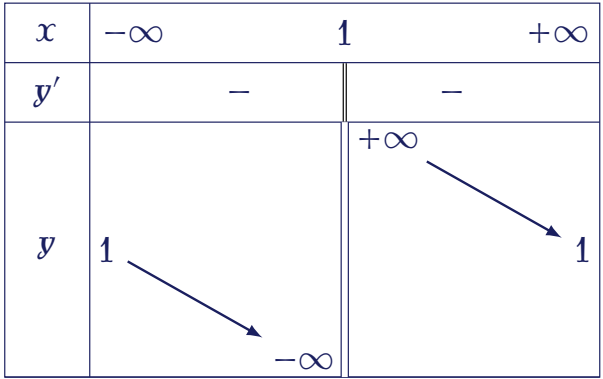
| $y=-x^3+3x+1$ | |
| $y=\dfrac{x-1}{x+1}$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^4-x^2+1$ |
Giá trị nhỏ nhất của hàm số $f(x)=x^4-10x^2+2$ trên đoạn $[-1;2]$ bằng
| $-1$ | |
| $2$ | |
| $-23$ | |
| $-22$ |
Hàm số $y=x^4-2x^2-1$ có bao nhiêu điểm cực trị?
| $2$ | |
| $1$ | |
| $0$ | |
| $3$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\big\{0;1\big\}$ | |
| $\big\{1\big\}$ | |
| $\big\{-1;1\big\}$ | |
| $\big\{0\big\}$ |
Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?
| $y=x^3-2x^2-1$ | |
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^4+2x^2+1$ |
Hàm số nào dưới đây nghịch biến trên tập $\mathbb{R}$?
| $y=3x^3-x$ | |
| $y=-2x^4-x$ | |
| $y=-2x^3+3$ | |
| $y=-x^4+2$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=(m+2)x^4+(m-3)x^2+2022$ có ba cực trị là
| $4$ | |
| $2$ | |
| $3$ | |
| $6$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
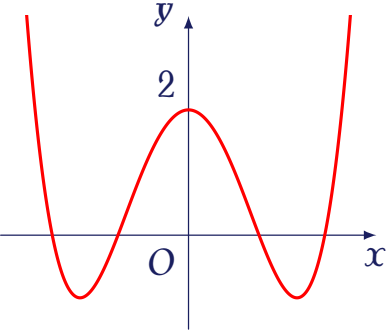
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Hàm số nào sau đây có đồ thị như đường cong trong hình bên dưới?
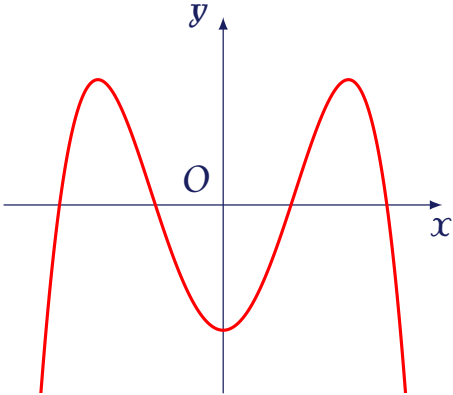
| $y=-x^4+3x^2-1$ | |
| $y=x^4-3x^2-1$ | |
| $y=x^3-x^2-1$ | |
| $y=-x^3+x^2-1$ |
Cho hàm số $f(x)=x^4-32x^2+4$. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, tổng giá trị các nghiệm phân biệt thuộc khoảng $(-3;2)$ của phương trình $f\big(x^2+2x+3\big)=m$ bằng $-4$?
| $145$ | |
| $142$ | |
| $144$ | |
| $143$ |
Hàm số nào dưới đây có bảng biến thiên như sau?
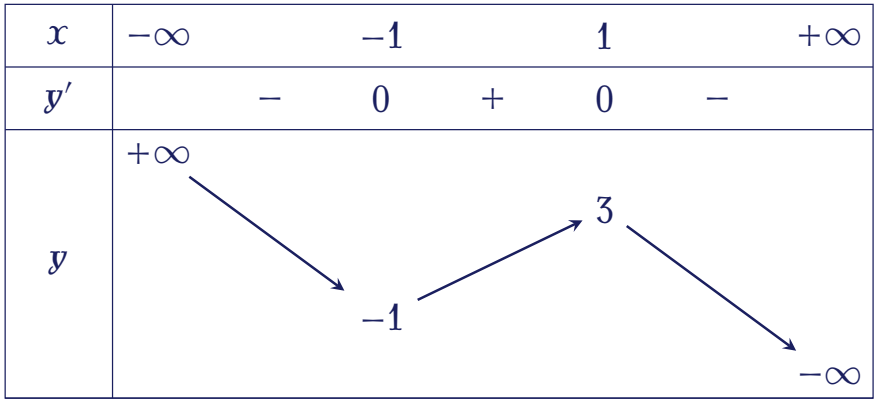
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
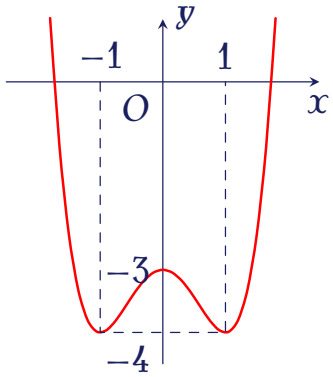
| $y=-x^4+2x^2-3$ | |
| $y=-x^3+3x$ | |
| $y=x^4-2x^2-3$ | |
| $y=x^3-3x-3$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
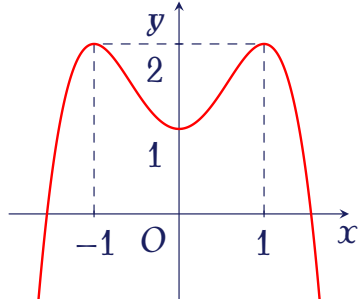
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
| $(-1;2)$ | |
| $(0;1)$ | |
| $(1;2)$ | |
| $(1;0)$ |
Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
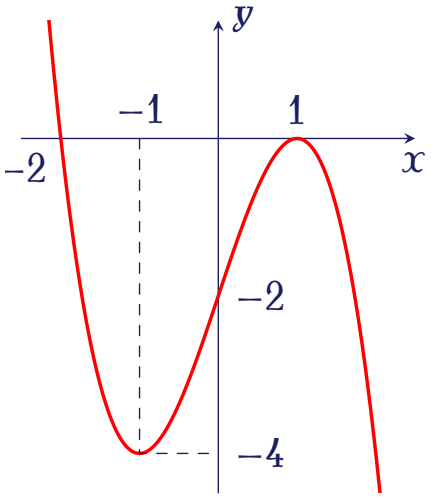
| $y=-x^3+3x-2$ | |
| $y=x^3-3x+2$ | |
| $y=x^4-3x^2-2$ | |
| $y=x^4-3x^2+2$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\{0;1\}$ | |
| $\{1\}$ | |
| $\{-1;1\}$ | |
| $\{0\}$ |
Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?
| $y=x^3-2x^2-1$ | |
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^4+2x^2+1$ |
Cho hàm số $f(x)=(m-1)x^4-2mx^2+1$ với $m$ là tham số thực. Nếu $\min\limits_{[0;3]}f(x)=f(2)$ thì $\max\limits_{[0;3]}f(x)$ bằng
| $-\dfrac{13}{3}$ | |
| $4$ | |
| $-\dfrac{14}{3}$ | |
| $1$ |
