Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\) và \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([a;b]\). Mệnh đề nào dưới đây đúng?
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(a)-F(b)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(b)-f(a)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=f(a)-f(b)\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=F(b)-F(a)\) |
Biết \(F(x)\) là một nguyên hàm của \(f(x)\) trên đoạn \([-2;3]\), \(\displaystyle\int\limits_{-2}^3f(x)\mathrm{\,d}x=12\) và \(F(3)=7\). Tính \(F(-2)\).
| \(F(-2)=19\) | |
| \(F(-2)=2\) | |
| \(F(-2)=5\) | |
| \(F(-2)=-5\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\) và \(a< c< b\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x=\displaystyle\int\limits_b^c f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x+\displaystyle\int\limits_c^b f(x)\mathrm{\,d}x=\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=-\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x=0\) |
Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên đoạn \([a;b]\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_a^b[f(x)-g(x)]\mathrm{\,d}x = \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x - \displaystyle\int\limits_a^b g(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b kf(x)\mathrm{\,d}x =k \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) với \(k\) là hằng số | |
| \(\displaystyle\int\limits_a^b [f(x)\cdot {g(x)}]\mathrm{\,d}x=\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x \cdot {\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_a^b [f(x)+g(x)]\mathrm{\,d}x = \displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x\) |
Cho \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=-3\) và \(\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x=4\). Tính \(I=\displaystyle\int\limits_a^b [4f(x)-3g(x)]\mathrm{\,d}x\).
| \(I=25\) | |
| \(I=-24\) | |
| \(I=24\) | |
| \(I=0\) |
Cho \(\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x=5\) và \(\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x=2\). Tính \(I=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x\).
| \(I=7\) | |
| \(I=-3\) | |
| \(I=3\) | |
| \(I=1\) |
Tính \(I=\displaystyle\int\limits_0^2(2x-x^3)\mathrm{\,d}x\).
| \(I=0\) | |
| \(I=10\) | |
| \(I=-4\) | |
| \(I=-10\) |
Cho \(\displaystyle\int\limits_{-1}^5f(x)\mathrm{\,d}x=9\). Tính \(I=\displaystyle\int\limits_0^2f(3x-1)\mathrm{\,d}x\).
| \(I=26\) | |
| \(I=9\) | |
| \(I=3\) | |
| \(I=27\) |
Tính \(I=\displaystyle\int\limits_0^{\tfrac{\pi}{3}}\sin{2x}\mathrm{\,d}x\).
| \(I=-\dfrac{1}{4}\) | |
| \(I=0,019\) | |
| \(I=-\dfrac{3}{4}\) | |
| \(I=\dfrac{3}{4}\) |
Biết \(\displaystyle\int\limits_{\ln2}^{\ln5}(x+1)\mathrm{e}^x \mathrm{\,d}x=a\ln5+b\ln2\), với \(a,\,b\) là các số nguyên. Tính \(T=3a-2b\).
| \(T=19\) | |
| \(T=-4\) | |
| \(T=11\) | |
| \(T=-16\) |
Cho hình phẳng \(D\) giới hạn bởi đồ thị hai hàm số \(y=f(x),\,y=g(x)\) liên tục trên đoạn \([a;b]\) và hai đường thẳng \(x=a,\,x=b\). Diện tích \(S\) của hình phẳng \(D\) là
| \(S=\displaystyle\int\limits_a^b[f(x)+g(x)]\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b |f(x)-g(x)|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b[f(x)-g(x)]\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_a^b[g(x)-f(x)]\mathrm{\,d}x\) |
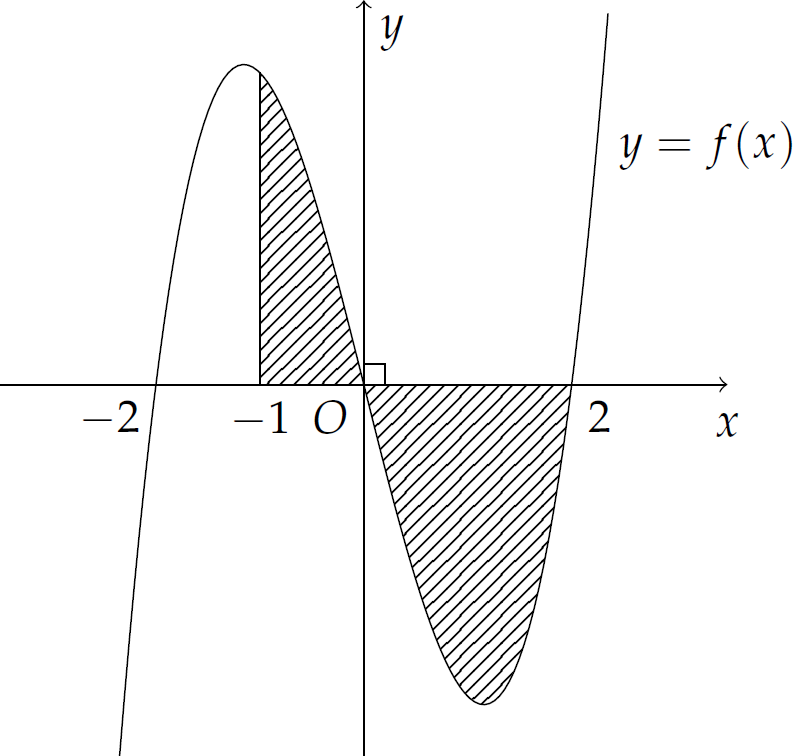
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y=f(x)\) trục \(Ox\) và đường thẳng \(x=-1\) (phần gạch sọc như hình trên). Gọi \(S\) là diện tích của hình phẳng \(H\). Mệnh đề nào dưới đây đúng?
| \(S=\displaystyle\int\limits_{-1}^0|f(x)|\mathrm{\,d}x-\displaystyle\int\limits_0^2|f(x)|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x-\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x+\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=3^x\), trục \(Ox\) và hai đường thẳng \(x=-1\), \(x=2\).
| \(S=\dfrac{26}{3}\) | |
| \(S=12\) | |
| \(S=\dfrac{12}{\ln3}\) | |
| \(S=\dfrac{26}{3\ln3}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2+x\) và đường thẳng \(y=-x+3\).
| \(S=-\dfrac{32}{3}\) | |
| \(S=\dfrac{16}{3}\) | |
| \(S=16\) | |
| \(S=\dfrac{32}{3}\) |
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\), trục \(Ox\) và hai đường thẳng \(x=a,\,x=b\). Thể tích \(V\) của khối tròn xoay được tạo thành khi quay \(H\) quanh trục \(Ox\) là
| \(V=\pi\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_a^b|f(x)|\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x\) |
Cho hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(y=2x^2+3x\), trục \(Ox\) và hai đường thẳng \(x=0,\,x=1\). Tính thể tích \(V\) của khối tròn xoay được tạo thành khi quay \(D\) quanh trục \(Ox\).
| \(V=\dfrac{13}{6}\) | |
| \(V=\dfrac{13\pi}{6}\) | |
| \(V=\dfrac{34\pi}{5}\) | |
| \(V=\dfrac{34}{5}\) |
Tìm phần thực và phần ảo của số phức \(z=2-3i\).
| Phần thực là \(2\) và phần ảo là \(3\) | |
| Phần thực là \(2\) và phần ảo là \(-3\) | |
| Phần thực là \(2\) và phần ảo là \(3i\) | |
| Phần thực là \(2\) và phần ảo là \(-3i\) |
Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z=5-i\).
| \(M(5;0)\) | |
| \(M(5;-1)\) | |
| \(M(0;-5)\) | |
| \(M(5;1)\) |
Cho số phức \(z=(2m-1)+(m^2-4)i\), \(m\in\mathbb{R}\). Tìm \(m\) để số phức \(z\) là số thuần ảo.
| \(m=2,\,m=-2\) | |
| \(m=2\) | |
| \(m=-\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{2}\) |
Cho hai số phức \(z_1=3+2i\) và \(z_2=1-5i\). Tìm phần thực và phần ảo của số phức \(z_1+z_2\).
| Phần thực là \(4\) và phần ảo là \(3\) | |
| Phần thực là \(4\) và phần ảo là \(-3i\) | |
| Phần thực là \(4\) và phần ảo là \(3i\) | |
| Phần thực là \(4\) và phần ảo là \(-3\) |
Cho hai số phức \(z_1=-4+\sqrt{2}i\) và \(z_2=1-\sqrt{3}i\). Tìm phần ảo của số phức \(z_1-z_2\).
| Phần ảo là \(\sqrt{5}\) | |
| Phần ảo là \(\sqrt{2}-\sqrt{3}\) | |
| Phần ảo là \(\sqrt{2}+\sqrt{3}\) | |
| Phần ảo là \(-5\) |
Cho hai số phức \(z_1=\dfrac{1}{2}-2i\) và \(z_2=4-i\). Tính môđun của số phức \(z=z_1\cdot z_2\).
| \(|z|=\dfrac{\sqrt{34}}{2}\) | |
| \(|z|=\dfrac{289}{4}\) | |
| \(|z|=\dfrac{17}{2}\) | |
| \(|z|=-\dfrac{17}{2}\) |
Tính môđun của số phức $$z=\dfrac{\left(-2-3i\right)\left(-1+2i\right)}{2+i}.$$
| \(|z|=\sqrt{13}\) | |
| \(|z|=\sqrt{5}\) | |
| \(|z|=13\) | |
| \(|z|=5\) |
Tìm phần thực và phần ảo của số phức $$z=\dfrac{6-3i}{2+5i}.$$
| Phần thực là \(-\dfrac{3}{29}\) và phần ảo là \(-\dfrac{36}{29}\) | |
| Phần thực là \(-\dfrac{3}{29}\) và phần ảo là \(-\dfrac{36}{29}i\) | |
| Phần thực là \(\dfrac{1}{7}\) và phần ảo là \(\dfrac{12}{7}\) | |
| Phần thực là \(\dfrac{1}{7}\) và phần ảo là \(\dfrac{12}{7}i\) |
Tìm số phức liên hợp của số phức $$z=(11-3i)+(5+2i)(1-i).$$
| \(\overline{z}=14+6i\) | |
| \(\overline{z}=18+6i\) | |
| \(\overline{z}=18-6i\) | |
| \(\overline{z}=14-6i\) |
Tìm số phức \(z\) thỏa mãn $$(3-5i)z+(2+3i)=-4i.$$
| \(z=\dfrac{2}{17}-\dfrac{8}{17}i\) | |
| \(z=\dfrac{29}{34}-\dfrac{31}{34}i\) | |
| \(z=\dfrac{1}{17}-\dfrac{21}{17}i\) | |
| \(z=-\dfrac{1}{34}-\dfrac{13}{34}i\) |
Tìm số phức \(z\) thỏa mãn $$z-1+4i=2i\overline{z}.$$
| \(z=\dfrac{9}{5}-\dfrac{2}{5}i\) | |
| \(z=-\dfrac{9}{5}+\dfrac{2}{5}i\) | |
| \(z=\dfrac{7}{3}+\dfrac{2}{3}i\) | |
| \(z=-\dfrac{7}{3}-\dfrac{2}{3}i\) |
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện \(|z-2+3i|=4\).
| Đường tròn tâm \(I(2;-3)\) và bán kính \(R=4\) | |
| Đường tròn tâm \(I(-2;3)\) và bán kính \(R=16\) | |
| Đường tròn tâm \(I(-2;3)\) và bán kính \(R=4\) | |
| Đường tròn tâm \(I(2;-3)\) và bán kính \(R=16\) |
Tìm một căn bậc hai của \(-8\).
| \(-2\sqrt{2}i\) | |
| \(-2\sqrt{2}\) | |
| \(2\sqrt{2}\) | |
| \(2\sqrt{-2}i\) |
Tìm nghiệm phức có phần ảo âm của phương trình $$z^2-4z+13=0.$$
| \(z=-2-3i\) | |
| \(z=2-3i\) | |
| \(z=-2+3i\) | |
| \(z=2+3i\) |
Kí hiệu \(z_0\) là nghiệm phức có phần ảo dương của phương trình \(2z^2-6z+15=0\). Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z_0\).
| \(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\) | |
| \(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\) | |
| \(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\) | |
| \(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\) |
Tìm tập nghiệm \(S\) của phương trình \(z^4-7z^2-18=0\) trên tập số phức.
| \(S=\left\{-2;9\right\}\) | |
| \(S=\left\{-\sqrt{2};\sqrt{2};-3i;3i\right\}\) | |
| \(S=\left\{-4i;4i;-81;81\right\}\) | |
| \(S=\left\{-3;3;-\sqrt{2}i;\sqrt{2}i\right\}\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A(-5;0;2)\), \(B(3;1;-1)\), \(C(0;0;7)\). Tìm tọa độ điểm \(M\) sao cho \(A\) là trọng tâm của tam giác \(MBC\).
| \(M\left(\dfrac{2}{3};\dfrac{1}{3};\dfrac{8}{3}\right)\) | |
| \(M(-18;-1;0)\) | |
| \(M(2;1;8)\) | |
| \(M(-12;-3;-10)\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow{a}=(1;-2;5)\) và \(\overrightarrow{b}=(-2;4;2)\). Tìm tọa độ của vectơ \(\overrightarrow{a}-\overrightarrow{b}\).
| \(\overrightarrow{a}-\overrightarrow{b}=(3;-2;3)\) | |
| \(\overrightarrow{a}-\overrightarrow{b}=(3;-6;3)\) | |
| \(\overrightarrow{a}-\overrightarrow{b}=(-3;6;-3)\) | |
| \(\overrightarrow{a}-\overrightarrow{b}=(1;-2;1)\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho ba vectơ \(\overrightarrow{a}=(1;2;-2)\), \(\overrightarrow{b}=(-4;0;1)\) và \(\overrightarrow{c}=(0;3;3)\). Tính \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\cdot\overrightarrow{c}\).
| \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\cdot{\overrightarrow{c}}=3\) | |
| \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\cdot{\overrightarrow{c}}=9\) | |
| \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\cdot{\overrightarrow{c}}=0\) | |
| \(\left(\overrightarrow{a}+\overrightarrow{b}\right)\cdot{\overrightarrow{c}}=-10\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \((S)\colon(x-7)^2+(y+3)^2+z^2=16\). Tìm tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \((S)\).
| \(I(-7;3;0)\) và \(R=4\) | |
| \(I(7;-3;0)\) và \(R=4\) | |
| \(I(-7;3;0)\) và \(R=16\) | |
| \(I(7;-3;0)\) và \(R=16\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của mặt cầu có tâm \(I(1;-3;-2)\) và đi qua điểm \(A(-5;0;2)\)?
| \((x+1)^2+(y-3)^2+(z-2)^2=61\) | |
| \((x+5)^2+y^2+(z-2)^2=61\) | |
| \((x-5)^2+y^2+(z+2)^2=61\) | |
| \((x-1)^2+(y+3)^2+(z+2)^2=61\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \((P)\colon2x-5y-8=0\). Tìm tọa độ một vectơ pháp tuyến của mặt phẳng \((P)\).
| \(\overrightarrow{n}=(2;-5;-8)\) | |
| \(\overrightarrow{n}=(2;-5;0)\) | |
| \(\overrightarrow{n}=(2;0;-5)\) | |
| \(\overrightarrow{n}=(-1;-2;0)\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm \(M(5;2;-1)\) và có vectơ pháp tuyến \(\overrightarrow{n}=(1;1;-2)\)?
| \(x+y-2z+9=0\) | |
| \(x+y-2z-9=0\) | |
| \(5x+2y-z+9=0\) | |
| \(5x+2y-z-9=0\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A(2;1;-1)\), \(B(-1;0;4)\) và \(C(0;-2;-1)\). Phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm \(A\) và vuông góc với đường thẳng \(BC\)?
| \(x-2y-5z-5=0\) | |
| \(x-2y-5z+5=0\) | |
| \(x-2y-5z-2=0\) | |
| \(2x+y-z-5=0\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm \(M(1;-2;0)\) và song song với mặt phẳng \((P)\colon x-y+3z-6=0\)?
| \(x-y+3z-1=0\) | |
| \(x-y+3z+1=0\) | |
| \(x-y+3z-3=0\) | |
| \(x-y+3z+3=0\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của mặt cầu có tâm \(I(3;-1;0)\) và tiếp xúc với mặt phẳng \((P)\colon x+2y-2z-10=0\)?
| \((x-3)^2+(y+1)^2+z^2=9\) | |
| \((x-3)^2+(y+1)^2+z^2=\dfrac{1}{9}\) | |
| \((x+3)^2+(y-1)^2+z^2=9\) | |
| \((x+3)^2+(y-1)^2+z^2=\dfrac{1}{9}\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta\colon\begin{cases}x=3\\y=2+2t\\z=1-3t\end{cases}\). Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\Delta\).
| \(M(0;2;-3)\) | |
| \(M(3;2;2)\) | |
| \(M(3;4;2)\) | |
| \(M(3;0;4)\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta\colon\begin{cases}x=2+t\\y=3-t\\z=1\end{cases}\). Tìm tọa độ một vectơ chỉ phương của \(\Delta\).
| \(\overrightarrow{u}=(1;-1;0)\) | |
| \(\overrightarrow{u}=(1;-1;1)\) | |
| \(\overrightarrow{u}=(2;3;1)\) | |
| \(\overrightarrow{u}=(2;3;0)\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của đường thẳng đi qua điểm \(M(2;-2;2)\) và có vectơ chỉ phương \(\overrightarrow{u}=(3;1;1)\)?
| \(\begin{cases}x=1+3t\\y=-1+t\\z=1+t\end{cases}\) | |
| \(\begin{cases}x=2+3t\\y=-2+t\\z=2+t\end{cases}\) | |
| \(\begin{cases}x=3+t\\y=1-t\\z=1+t\end{cases}\) | |
| \(\begin{cases}x=3+2t\\y=1-2t\\z=1+2t\end{cases}\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của đường thẳng đi qua hai điểm \(A(1;1;2)\) và \(B(6;11;-3)\)?
| \(\dfrac{x-5}{1}=\dfrac{y-10}{2}=\dfrac{z+5}{2}\) | |
| \(\dfrac{x+5}{1}=\dfrac{y+10}{2}=\dfrac{z-5}{2}\) | |
| \(\dfrac{x-1}{1}=\dfrac{y-1}{2}=\dfrac{z-2}{-1}\) | |
| \(\dfrac{x+1}{1}=\dfrac{y+1}{2}=\dfrac{z+2}{-1}\) |
Trong không gian với hệ tọa độ \(Oxyz\), phương trình nào dưới đây là phương trình của đường thẳng đi qua điểm \(M(0;4;1)\) và vuông góc với mặt phẳng \((P)\colon2x-2y-z=0\)?
| \(\begin{cases}x=-2\\y=2+4t\\z=1+t\end{cases}\) | |
| \(\begin{cases}x=2\\y=-2+4t\\z=-1+t\end{cases}\) | |
| \(\begin{cases}x=t\\y=4-t\\z=1-2t\end{cases}\) | |
| \(\begin{cases}x=2t\\y=4-2t\\z=1-t\end{cases}\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho hai đường thẳng \(\Delta\colon\dfrac{x}{1}=\dfrac{y+2}{2}=\dfrac{z-3}{-1}\) và \(\Delta'\colon\begin{cases}x=5-t\\y=-2t\\z=3+t\end{cases}\). Mệnh đề nào dưới đây đúng?
| \(\Delta\) song song với \(\Delta'\) | |
| \(\Delta\) trùng với \(\Delta'\) | |
| \(\Delta\) vuông góc với \(\Delta'\) | |
| \(\Delta\) và \(\Delta'\) chéo nhau |
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta\colon\dfrac{x+4}{2}=\dfrac{y+2}{1}=\dfrac{z-3}{3}\) và mặt phẳng \((P)\colon4x+2y+(m-1)z+13=0\). Tìm giá trị của \(m\) để \((P)\) vuông góc với \(\Delta\).
| \(m=-7\) | |
| \(m=7\) | |
| \(m=-\dfrac{7}{3}\) | |
| \(m=\dfrac{7}{3}\) |
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \((P)\colon4x-3y+z-13=0\) và điểm \(M(5;-5;4)\). Tìm tọa độ điểm \(M'\) đối xứng với \(M\) qua mặt phẳng \((P)\).
| \(M'(7;-9;10)\) | |
| \(M'(1;-2;3)\) | |
| \(M'(5;-5;4)\) | |
| \(M'(-3;1;2)\) |
