Cho hàm số \(y=-x^4+2x^2+3\) có giá trị cực đại và giá trị cực tiểu lần lượt là \(y_1,\,y_2\). Khi đó \(y_1+y_2\) bằng

	\(7\)
	\(1\)
	\(3\)
	\(-1\)

Hàm số \(y=x^3-9x^2+1\) có hai điểm cực trị là \(x_1,\,x_2\). Tính \(x_1+x_2\).

	\(6\)
	\(-10\)
	\(0\)
	\(-107\)

Cho hàm số \(y=x+\sqrt{12-3x^2}\). Khẳng định nào sau đây đúng?

	Hàm số đạt cực đại tại \(x=-1\)
	Hàm số đạt cực đại tại \(x=1\)
	Hàm số đạt cực tiểu tại \(x=-1\)
	Hàm số đạt cực tiểu tại \(x=1\)

Tìm điểm cực đại của đồ thị hàm số $$y=\dfrac{x}{2}+\dfrac{2}{x}$$

	\(N(-2;-2)\)
	\(x=-2\)
	\(M(2;2)\)
	\(x=2\)

Điểm cực đại của hàm số \(y=x^4-8x^2-3\) là

	\(S(0;-3)\)
	\(x=0\)
	\(x=\pm2\)
	\(y=0\)

Điểm cực tiểu của đồ thị hàm số \(y=-x^3+x^2+5x-5\) là

	\(E(-1;-8)\)
	\(G(0;-5)\)
	\(F\left(\dfrac{5}{3};\dfrac{40}{27}\right)\)
	\(H(1;0)\)

Cho hàm số \(y=\dfrac{x^3}{3}-x-1\). Giá trị cực tiểu của hàm số là

	\(2\)
	\(-\dfrac{1}{3}\)
	\(-\dfrac{5}{3}\)
	\(-1\)

Đồ thị hàm số \(y=-x^3+3x\) có điểm cực tiểu là

	\(M(-1;0)\)
	\(N(1;0)\)
	\(Q(1;-2)\)
	\(P(-1;-2)\)

Điểm cực tiểu của đồ thị hàm số \(y=x^3-3x+5\) là

	\(M(1;3)\)
	\(N(-1;7)\)
	\(Q(3;1)\)
	\(P(7;-1)\)

Tìm cực trị của hàm số $$y=2x^3+3x^2+4$$

	\(x_{\text{CĐ}}=-1,\;x_{\text{CT}}=0\)
	\(y_{\text{CĐ}}=5,\;y_{\text{CT}}=4\)
	\(x_{\text{CĐ}}=0,\;x_{\text{CT}}=-1\)
	\(y_{\text{CĐ}}=4,\;y_{\text{CT}}=5\)

Tìm điểm cực tiểu của hàm số $$y=x^3-3x^2-9x+2$$

	\(x=25\)
	\(x=3\)
	\(x=7\)
	\(x=-1\)

Cho hàm số \(f\left(x\right)=\dfrac{x+m}{x+1}\) (\(m\) là tham số thực). Gọi \(S\) là tập hợp tất cả các giá trị của m sao cho $$\max\limits_{[0;1]}\left|f\left(x\right)\right|+\min\limits_{[0;1]}\left|f\left(x\right)\right|=2.$$Số phần tử của \(S\) là

	\(6\)
	\(2\)
	\(1\)
	\(4\)

Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:

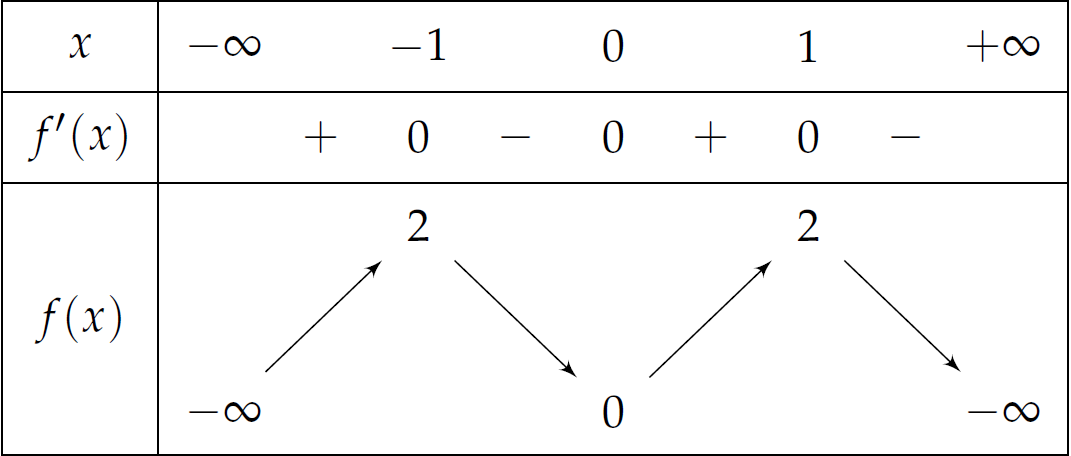
Số nghiệm thuộc đoạn \(\left[0;\dfrac{5\pi}{2}\right]\) của phương trình \(f\left(\sin x\right)=1\) là

	\(7\)
	\(4\)
	\(5\)
	\(6\)

Cho hàm số \(f\left(x\right)=\dfrac{ax+1}{bx+c}\) \(\left(a,b,c\in\mathbb{R}\right)\) có bảng biến thiên như sau:

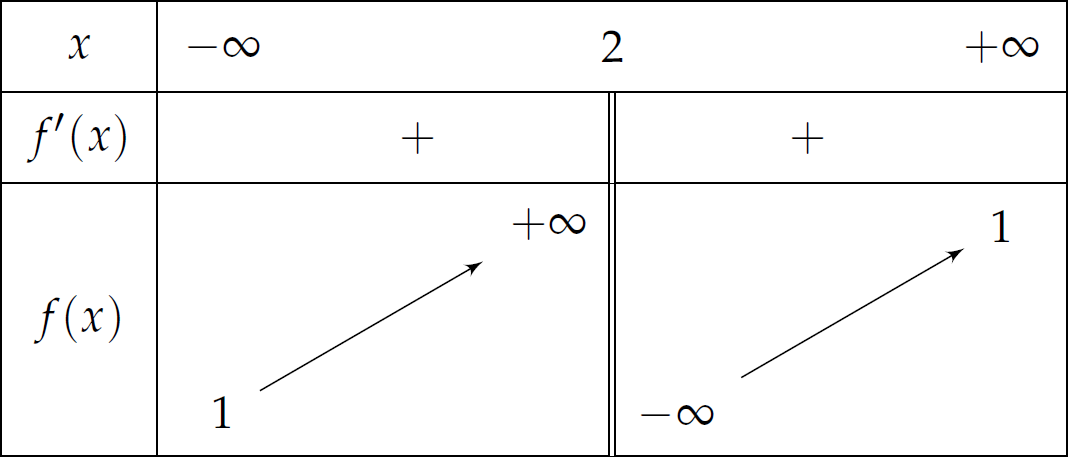
Trong các số \(a,\,b\) và \(c\) có bao nhiêu số dương?

	\(2\)
	\(3\)
	\(1\)
	\(0\)

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số $$f\left(x\right)=\dfrac{1}{3}x^3+mx^2+4x+3$$đồng biến trên \(\mathbb{R}\)?

	\(5\)
	\(4\)
	\(3\)
	\(2\)

Số giao điểm của đồ thị hàm số \(y=x^3-3x+1\) và trục hoành là

	\(3\)
	\(0\)
	\(2\)
	\(1\)

Giá trị nhỏ nhất của hàm số \(y=x^4-10x^2+2\) trên đoạn \(\left[-1;2\right]\) bằng

	\(2\)
	\(-23\)
	\(-22\)
	\(-7\)

Cho hàm số \(f\left(x\right)\) có bảng xét dấu của \(f'\left(x\right)\) như sau:

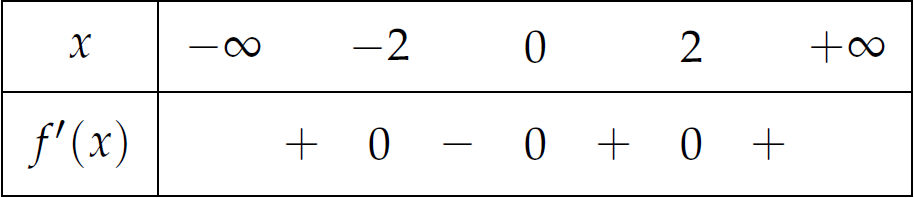
Số điểm cực trị của hàm số đã cho là

	\(3\)
	\(0\)
	\(2\)
	\(1\)

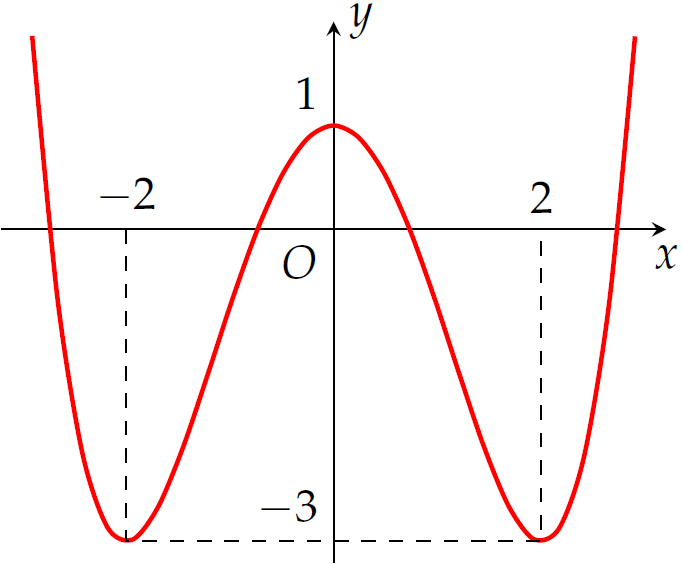
Cho hàm số \(y=f\left(x\right)\) có đồ thị trong hình vẽ trên. Số nghiệm của phương trình \(f\left(x\right)=-1\) là

	\(3\)
	\(2\)
	\(1\)
	\(4\)

Tiệm cận ngang của đồ thị hàm số \(y=\dfrac{x-2}{x+1}\) là

	\(y=-2\)
	\(y=1\)
	\(x=-1\)
	\(x=2\)