Với $b,\,c$ là hai số thực dương tùy ý thỏa mãn $\log_5b\ge\log_5c$, khẳng định nào dưới đây là đúng?
| $b\ge c$ | |
| $b\le c$ | |
| $b>c$ | |
| $b< c$ |
Cho các hàm số \(y=\log_ax\), \(y=b^x\), \(y=c^x\) có đồ thị như hình vẽ.
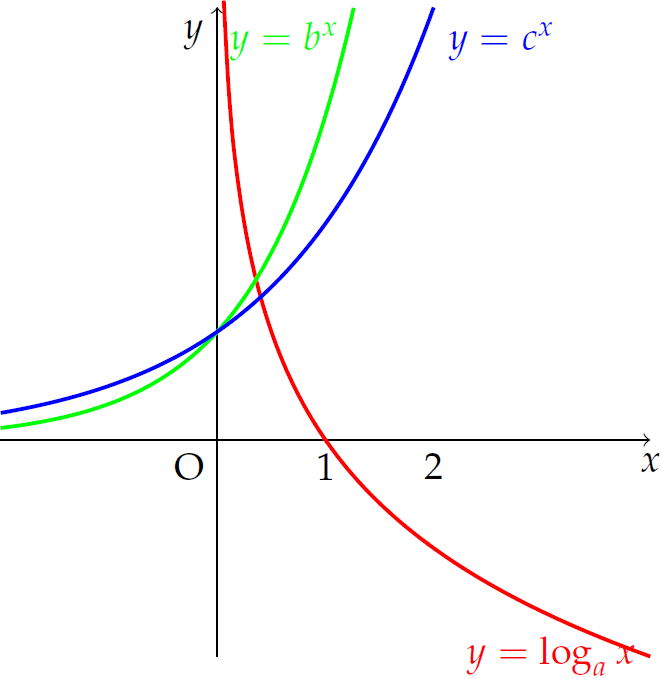
Mệnh đề nào dưới đây là đúng?
| \(b>c>a\) | |
| \(a>b>c\) | |
| \(b>a>c\) | |
| \(c>b>a\) |
Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).
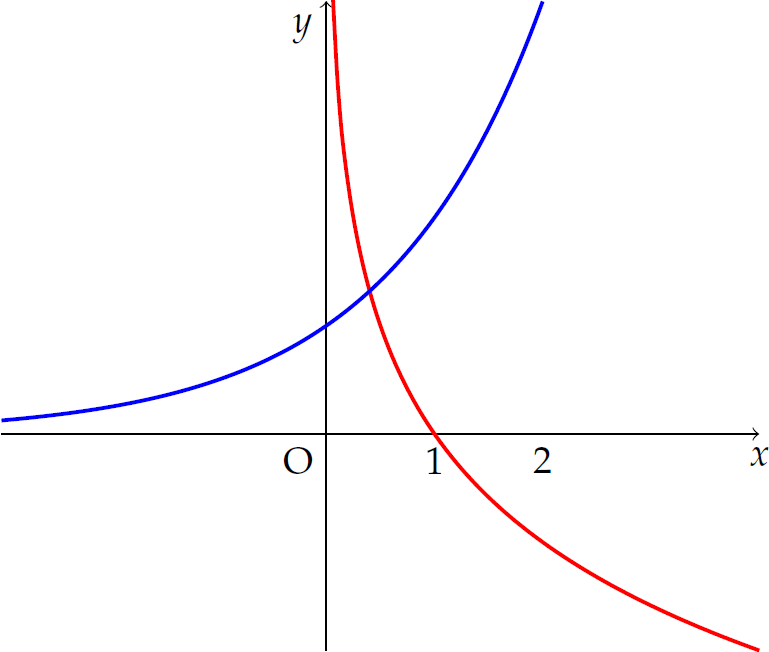
Mệnh đề nào dưới đây là đúng?
| \(\log_ab^2>0\) | |
| \(\log_ab<0\) | |
| \(\log_ab>0\) | |
| \(\log_ba>0\) |
Cho \(a,\,b,\,c\) dương và khác \(1\). Đồ thị hàm số \(y=\log_ax\), \(y=\log_bx\) và \(y=\log_cx\) được cho trong hình vẽ.
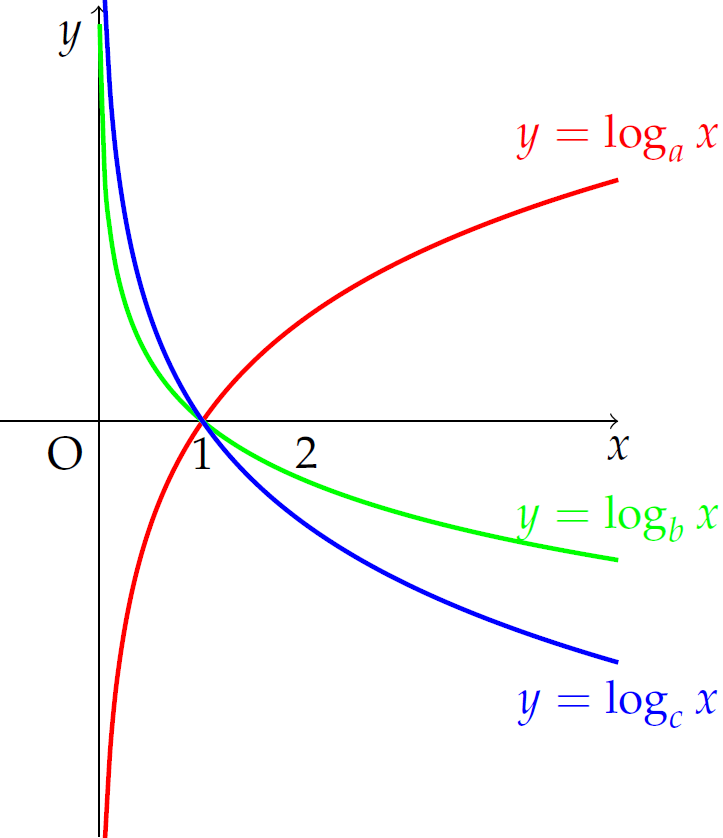
Khẳng định nào dưới đây là đúng?
| \(a>c>b\) | |
| \(b>c>a\) | |
| \(c>b>a\) | |
| \(a>b>c\) |
Cho \(a,\,b\) là hai số thực thỏa mãn \(0< a< b<1\). Mệnh đề nào dưới đây đúng?
| \(\log_ab<1<\log_ba\) | |
| \(\log_ba<1<\log_ab\) | |
| \(\log_ab<\log_ba<1\) | |
| \(1<\log_ab<\log_ba\) |
Cho các số thực dương \(a,\,b\) với \(a\neq1\). Khẳng định nào sau đây là đúng?
| \(\log_ab>0\Leftrightarrow\left[\begin{array}{l}0< a,\,b<1\\ 0< a<1< b\end{array}\right.\) | |
| \(\log_ab>0\Leftrightarrow\left[\begin{array}{l}0< a,\,b<1\\ a,\,b>1\end{array}\right.\) | |
| \(\log_ab>0\Leftrightarrow\left[\begin{array}{l}0< a,\,b<1\\ 0< b<1< a\end{array}\right.\) | |
| \(\log_ab>0\Leftrightarrow\left[\begin{array}{l}a,\,b>1\\ 0< b<1< a\end{array}\right.\) |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\ln\big(x^2-2x+m+1\big)$ có tập xác định là $\mathbb{R}$.
| $m=0$ | |
| $m< -1$ hoặc $m>0$ | |
| $m>0$ | |
| $0< m< 3$ |
Cho $\log3=a$ và $\log5=b$. Tính $\log_61125$ theo $a$ và $b$.
| $\dfrac{3a+2b}{a+1-b}$ | |
| $\dfrac{3a-2b}{a+1+b}$ | |
| $\dfrac{2a+3b}{a+1-b}$ | |
| $\dfrac{3a+2b}{a-1+b}$ |
Tìm tập xác định của hàm số $y=\log_{2023}\big(3x-x^2\big)$.
| $\mathscr{D}=(0;+\infty)$ | |
| $\mathscr{D}=(-\infty;0)\cup(3;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(0;3)$ |
Nếu $\log_8p=m$ và $\log_{p^3}3=n$ thì giá trị của tích $m\cdot n$ bằng
| $9\log_23$ | |
| $\dfrac{1}{9}\log_23$ | |
| $9\log_32$ | |
| $\dfrac{1}{9}\log_32$ |
Tập nghiệm của phương trình $\log_2(x-1)+2\log_4(3x+7)=5$ là
| $S=\left\{\dfrac{13}{3}\right\}$ | |
| $S=\big\{3\big\}$ | |
| $S=\big\{-3\big\}$ | |
| $S=\left\{3;-\dfrac{13}{3}\right\}$ |
Cho hàm số $f(x)=\ln\big(x^2+1\big)$. Giá trị $f'(2)$ bằng
| $\dfrac{4}{5}$ | |
| $\dfrac{4}{3\ln2}$ | |
| $\dfrac{4}{2\ln5}$ | |
| $2$ |
Với $a>0$ và $a\neq1$, khi đó $\log_a\sqrt[7]{a}$ bằng
| $-\dfrac{1}{7}$ | |
| $\dfrac{1}{7}$ | |
| $-7$ | |
| $7$ |
Nghiệm của phương trình $\log_2(3x-2)=0$ là
| $x=2$ | |
| $x=\dfrac{5}{3}$ | |
| $x=\dfrac{4}{3}$ | |
| $x=1$ |
Cho số thực $m$ sao cho đường thẳng $x=m$ cắt đồ thị hàm số $y=\log_2x$ tại $A$ và đồ thị hàm số $y=\log_2(x+3)$ tại $B$ thỏa mãn $AB=3$. Khẳng định nào dưới đây đúng?
| $m\in\left(\dfrac{1}{3};\dfrac{1}{2}\right)$ | |
| $m\in\left(0;\dfrac{1}{3}\right)$ | |
| $m\in\left(\dfrac{2}{3};1\right)$ | |
| $m\in\left(\dfrac{1}{2};\dfrac{2}{3}\right)$ |
Gọi $x_1,\,x_2$ là các nghiệm của phương trình $2\log2+2\log(x+2)=\log x+4\log3$. Tích $x_1x_2$ bằng
| $\dfrac{15}{2}$ | |
| $\dfrac{9}{2}$ | |
| $6$ | |
| $4$ |
Cho các số thực $a>1$, $b>1$, $c>1$ thỏa mãn $\dfrac{2}{\log_ac^6}+\dfrac{3}{\log_bc^6}=\dfrac{1}{3}$. Đẳng thức nào dưới đây đúng?
| $a^2b^2=c^3$ | |
| $a^2b^3=c^2$ | |
| $a^3b^2=c^2$ | |
| $a^3b^2=c$ |
Cho các số thực dương $x,\,y$ thỏa mãn $\ln x+\ln y\geq\ln\big(2x+y^2\big)$. Tìm giá trị nhỏ nhất của biểu thức $S=x+8y$.
| $32$ | |
| $29$ | |
| $25$ | |
| $46$ |
Tập nghiệm của phương trình $\log_2(x-1)+\log_2(x+3)=3$ là
| $\big\{-1+2\sqrt{3}\big\}$ | |
| $\big\{-1+2\sqrt{3};\,-1-2\sqrt{3}\big\}$ | |
| $\big\{-1+\sqrt{10}\big\}$ | |
| $\big\{-1+\sqrt{10};\,-1-\sqrt{10}\big\}$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
