Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).
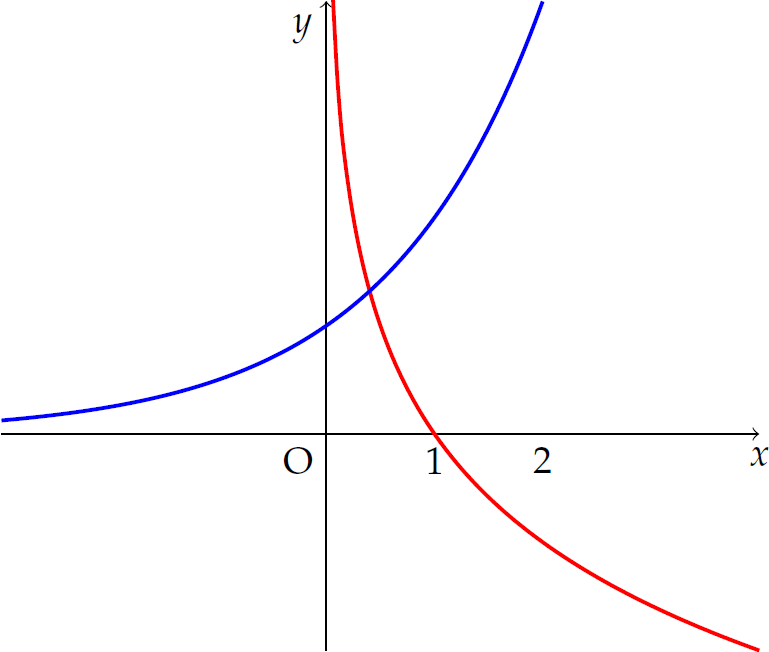
Mệnh đề nào dưới đây là đúng?
| \(\log_ab^2>0\) | |
| \(\log_ab<0\) | |
| \(\log_ab>0\) | |
| \(\log_ba>0\) |
Cho ba số thực dương \(a,\,b,\,c\) khác \(1\). Đồ thị hàm số \(y=a^x\), \(y=b^x\) và \(y=c^x\) được cho trong hình vẽ.
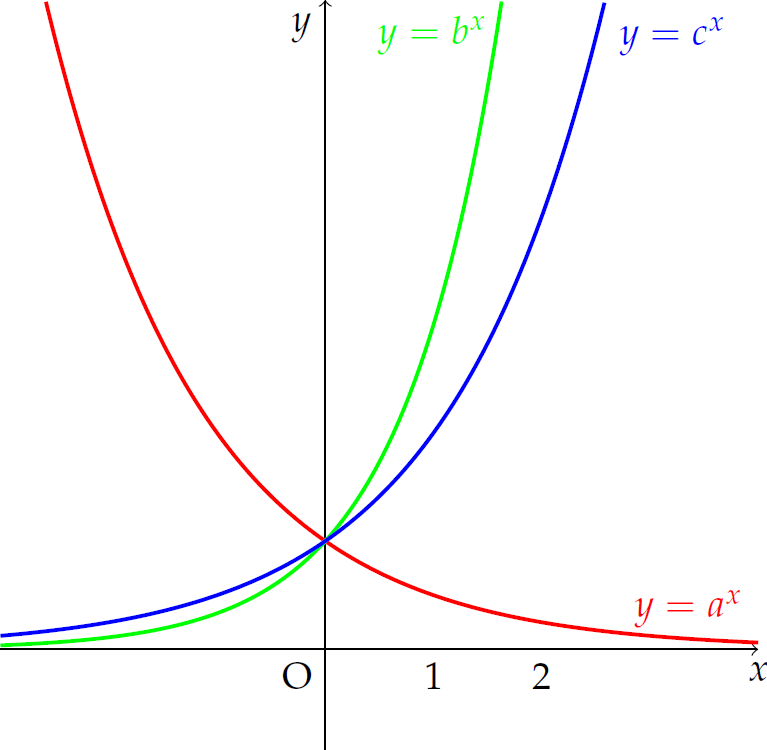
Mệnh đề nào dưới đây là đúng?
| \(a< b< c\) | |
| \(a< c< b\) | |
| \(b< c< a\) | |
| \(c< a< b\) |
Cho \(a,\,b,\,c\) dương và khác \(1\). Đồ thị hàm số \(y=\log_ax\), \(y=\log_bx\) và \(y=\log_cx\) được cho trong hình vẽ.
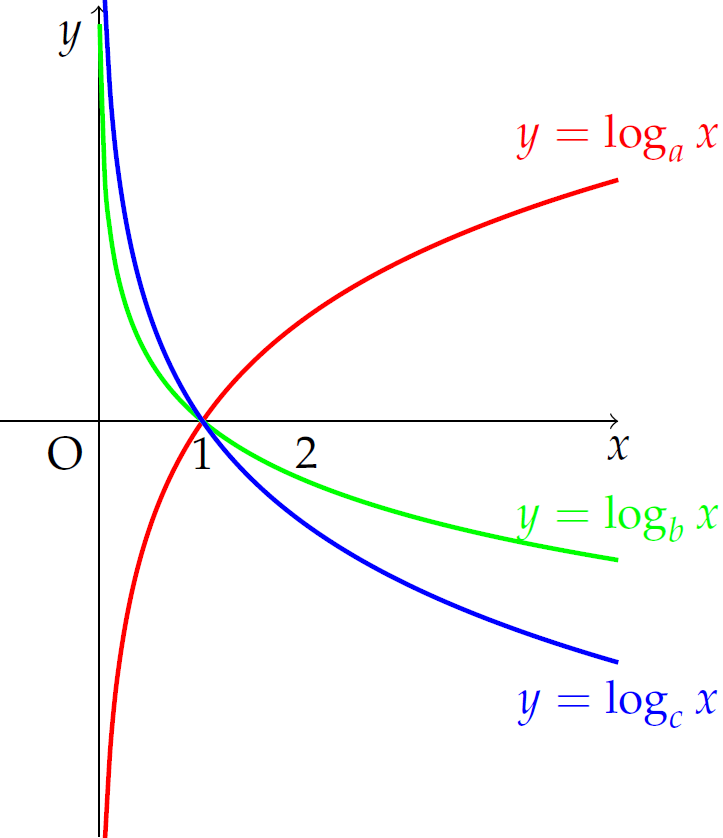
Khẳng định nào dưới đây là đúng?
| \(a>c>b\) | |
| \(b>c>a\) | |
| \(c>b>a\) | |
| \(a>b>c\) |
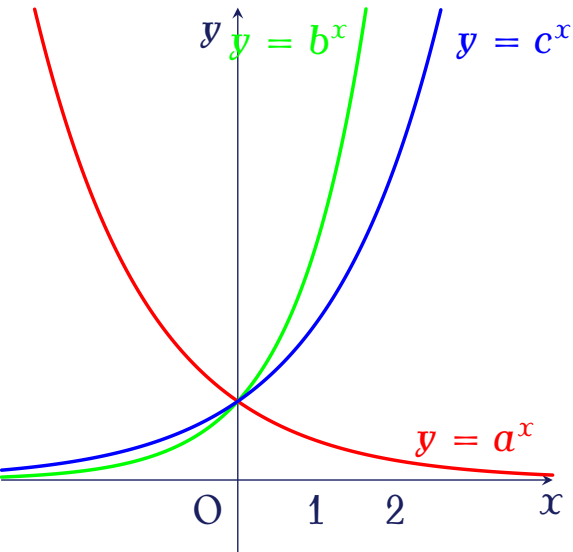
Cho đồ thị của các hàm số $y=a^x$, $y=b^x$, $y=c^x$ như hình bên.
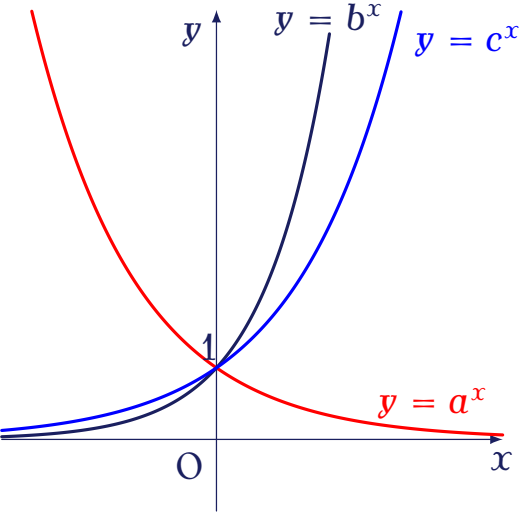
Hỏi trong các số $a,\,b$ và $c$ có bao nhiêu số lớn hơn $1$?
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Cho $a$ và $b$ là hai số thực dương khác $1$ và các hàm số $y=a^x$, $y=b^x$ có đồ thị như hình bên.
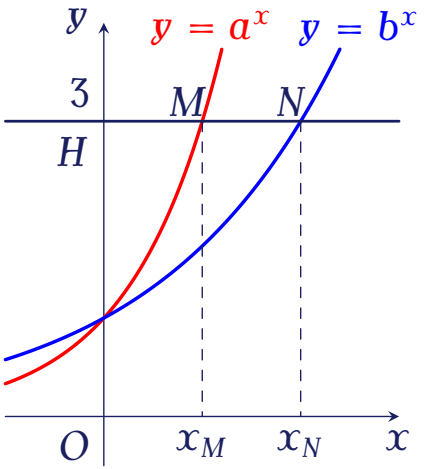
Đường thẳng $y=3$ cắt trục tung, đồ thị hàm số $y=a^x$, đồ thị hàm số $y=b^x$ lần lượt tại $H,\,M,\,N$. Biết rằng $HM=2MN$. Mệnh đề nào sau đây đúng?
| $a^2=b^3$ | |
| $3a=2b$ | |
| $a^3=b^2$ | |
| $2a=b$ |
Trong hình bên là đồ thị các hàm số $y=a^x$ và $y=b^x$.
Mệnh đề nào dưới đây là đúng?
| $0< a< 1< b$ | |
| $1< a< b$ | |
| $0< a< b< 1$ | |
| $0< b< 1< a$ |
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án $A,\,B,\,C,\,D$ dưới đây.
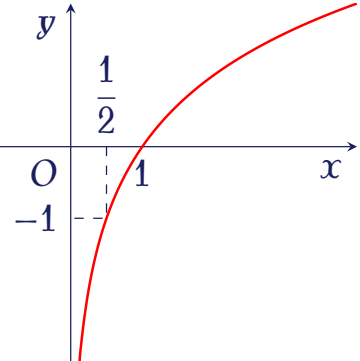
Hỏi hàm số đó là hàm số nào?
| $y=\log_2x$ | |
| $y=\log_{\sqrt{2}}x$ | |
| $y=\log_22x$ | |
| $y=\log_{\tfrac{1}{2}}x$ |
Cho hàm số $y=2^x$ có đồ thị là đường cong trong hình bên.
Diện tích $S$ của hình phẳng được tô đậm trong hình bằng
| $S=\displaystyle\displaystyle\int\limits_{1}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^{2x}\mathrm{\,d}x$ | |
| $S=\pi\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ |
Cho hàm số \(y=f(x)\) có đồ thị \(f'(x)\) như hình vẽ.
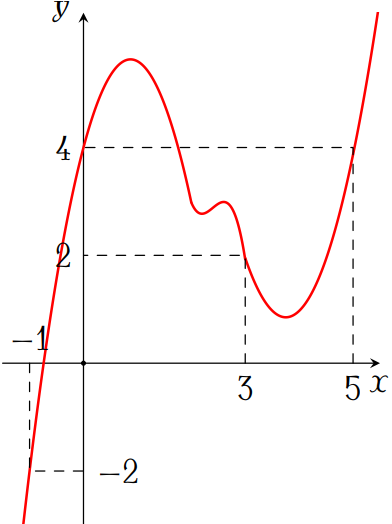
Đặt \(g(x)=2f(x)-(x-1)^2\). Mệnh đề nào dưới đây đúng?
| \(g(-1)< g(5)< g(3)\) | |
| \(g(3)< g(5)< g(-1)\) | |
| \(g(5)< g(-1)< g(3)\) | |
| \(g(-1)< g(3)< g(5)\) |
Biết hàm số \(f(x)=\dfrac{a}{b^2\cdot3^x}\) có đồ thị đối xứng với đồ thị hàm số \(y=3^x\) qua đường thẳng \(x=-1\). Biết \(a,\,b\) là các số nguyên.
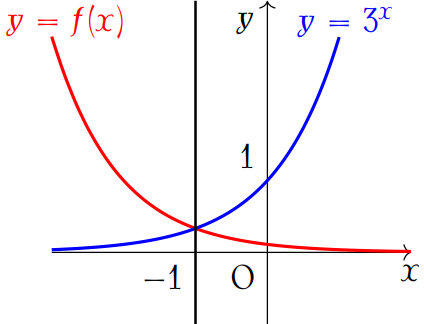
Chọn khẳng định đúng trong các khẳng định sau:
| \(b^2=9a\) | |
| \(b^2=4a\) | |
| \(b^2=6a\) | |
| \(b^2=a\) |
Đồ thị của hàm số \(y=x^2+4x+1\) là đường cong nào dưới đây?
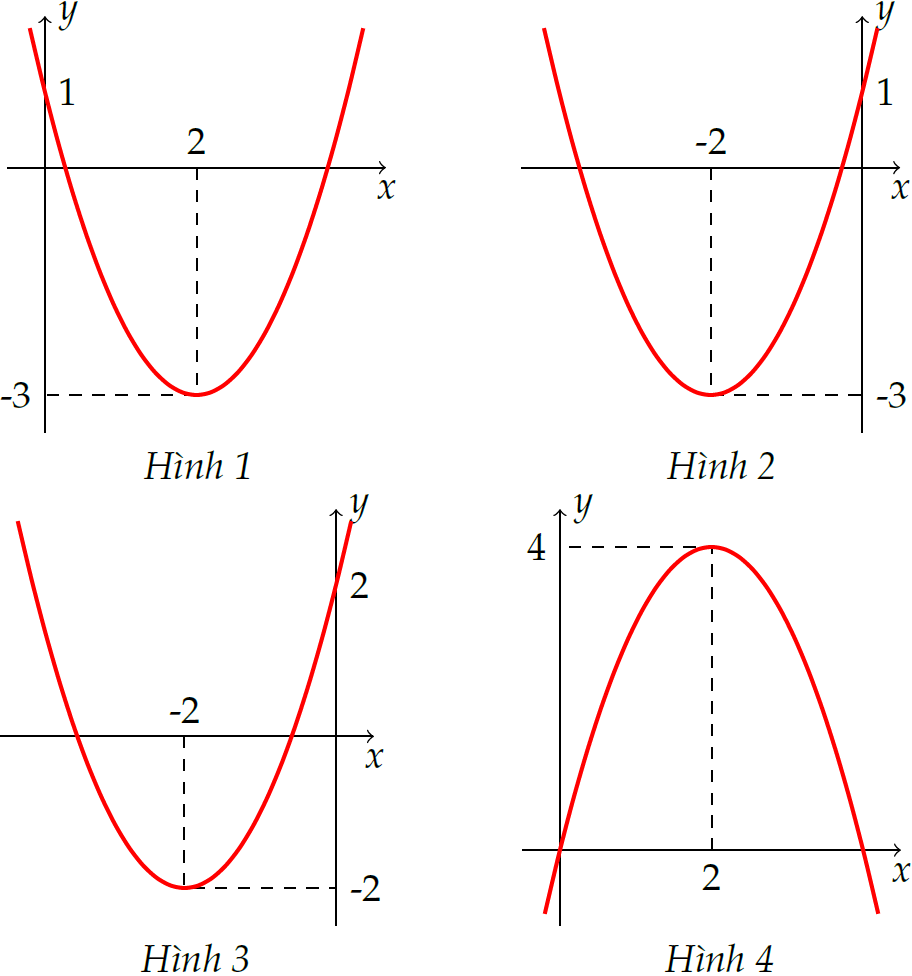
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Hình vẽ sau đây là đồ thị của hàm số nào?
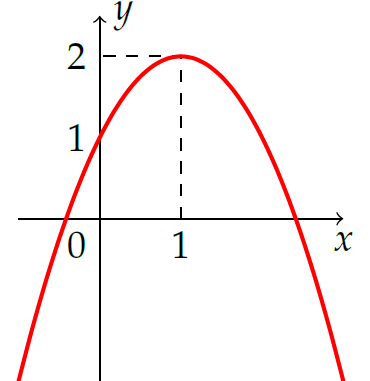
| \(y=-x^2+2x\) | |
| \(y=x^2-2x+1\) | |
| \(y=-x^2-2x+1\) | |
| \(y=-x^2+2x+1\) |
Hình vẽ sau đây là đồ thị của hàm số nào?
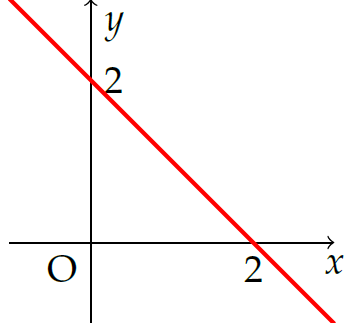
| \(y=2-x\) | |
| \(y=x-2\) | |
| \(y=2-2x\) | |
| \(y=1-2x\) |
Hình vẽ nào dưới đây là đồ thị của hàm số \(y=\dfrac{x}{2}-2\)?
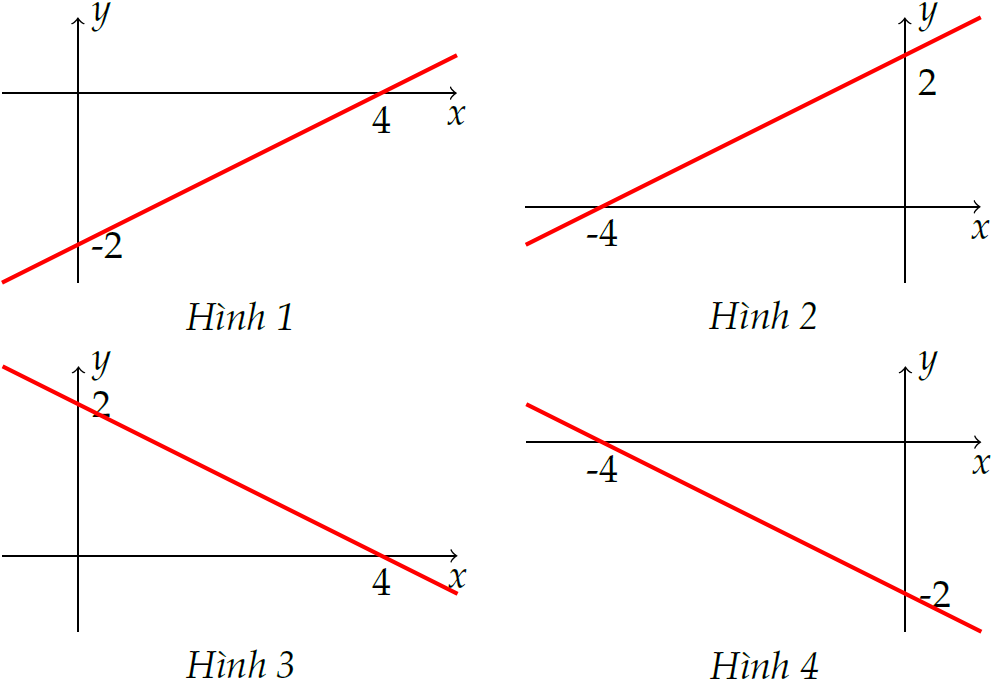
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình vẽ bên.
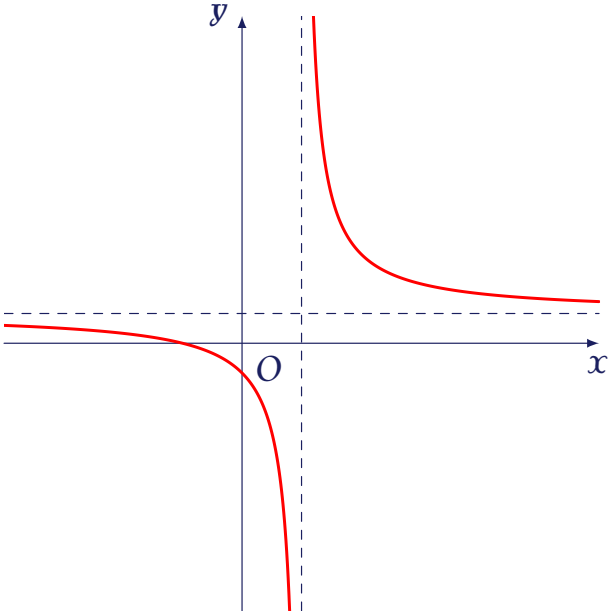
Kết luận nào sau đây đúng?
| $ad>0$, $bc< 0$ | |
| $ad< 0$, $bc>0$ | |
| $ad< 0$, $bc< 0$ | |
| $ad>0$, $bc>0$ |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong như hình vẽ bên dưới.
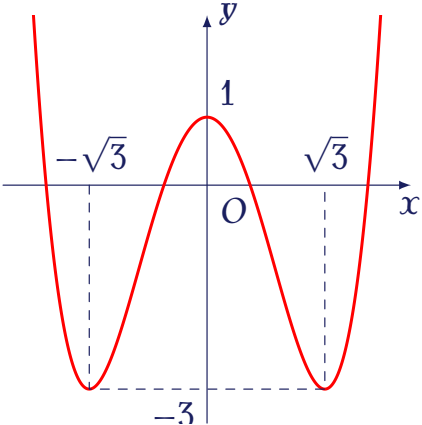
Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình $f(x)=m$ có bốn nghiệm thực phân biệt?
| $3$ | |
| $2$ | |
| $4$ | |
| $5$ |
Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số dưới đây.
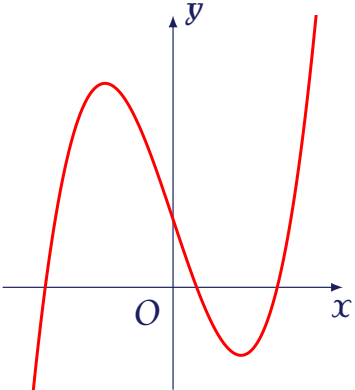
Hãy xác định hàm số đó.
| $y=-x^4-4x^2+1$ | |
| $y=x^3-3x+1$ | |
| $y=-x^3+3x-1$ | |
| $y=x^3+3x+1$ |
Hàm số nào dưới đây có bảng biến thiên như hình bên?
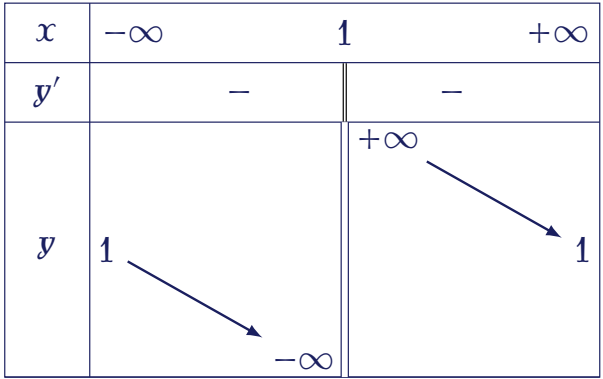
| $y=-x^3+3x+1$ | |
| $y=\dfrac{x-1}{x+1}$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^4-x^2+1$ |
Cho hàm số $y=f(x)$ là hàm đa thức bậc ba và có đồ thị như hình vẽ.
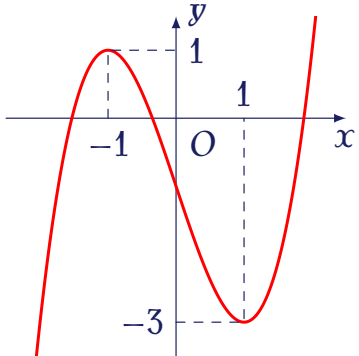
Khẳng định nào sau đây là sai?
| Hàm số đồng biến trên $(1;+\infty)$ | |
| Hàm số đồng biến trên $(-\infty;-1)\cup(1;+\infty)$ | |
| Hàm số đồng biến trên $(-\infty;-1)$ | |
| Hàm số nghịch biến trên $(-1;1)$ |
Cho hàm số $y=f(x)$ có đồ thị như hình vẽ.
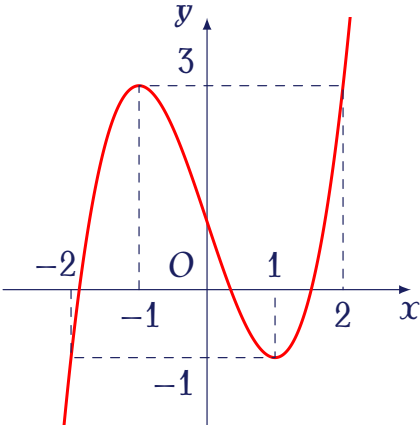
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
| $(-1;1)$ | |
| $(-2;0)$ | |
| $(-2;-1)$ | |
| $(0;2)$ |
