Hàm số nào dưới đây có bảng biến thiên như hình bên?

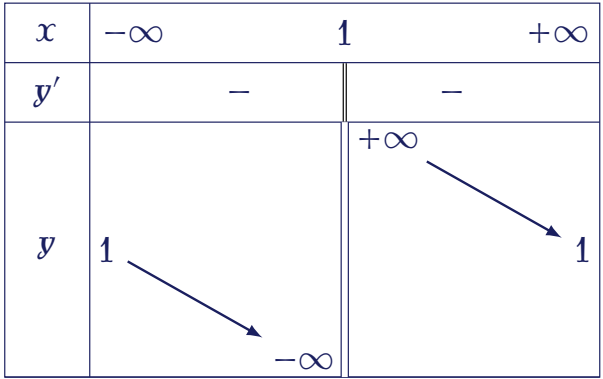
	$y=-x^3+3x+1$
	$y=\dfrac{x-1}{x+1}$
	$y=\dfrac{x+1}{x-1}$
	$y=x^4-x^2+1$

Trong các hàm số sau, hàm số nào không có cực trị?

	$y=x^2$
	$y=\dfrac{x+2}{2x-1}$
	$y=x^4+2x^2+2$
	$y=-x^3-x^2$

Hàm số nào dưới đây đồng biến trên $\mathbb{R}$?

	$y=x^4-x^2$
	$y=x^3-x$
	$y=\dfrac{x-1}{x+2}$
	$y=x^3+x$

Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?

	$y=-x^3-x$
	$y=-x^4-x^2$
	$y=-x^3+x$
	$y=\dfrac{x+2}{x-1}$

Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?

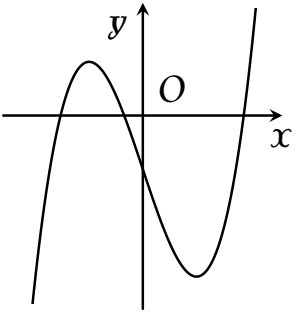
	$y=x^4-2x^2-1$
	$y=\dfrac{x+1}{x-1}$
	$y=x^3-3x-1$
	$y=x^2+x-1$

Hàm số nào dưới đây đồng biến trên $\mathbb{R}$?

	$y=\dfrac{x+1}{x-2}$
	$y=x^2+2x$
	$y=x^3-x^2+x$
	$y=x^4-3x^2+2$

Đồ thị hàm số nào dưới đây không có đường tiệm cận?

	\(y=\dfrac{x}{x^2+1}\)
	\(y=\dfrac{1}{x}\)
	\(y=x^4-3x^2+2\)
	\(y=\dfrac{2x+1}{2-x}\)

Hàm số nào sau đây không có cực trị?

	\(y=2x^3-3x^2\)
	\(y=x^4+2\)
	\(y=\dfrac{x+1}{x-2}\)
	\(y=-x^4+2x^2+1\)

Hàm số nào dưới đây đồng biến trên \((-\infty;+\infty)\)?

	\(y=\dfrac{x-1}{x}\)
	\(y=2x^3\)
	\(y=x^2+1\)
	\(y=x^4+5\)

Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?

	\(y=\sqrt{x^2-3x+2}\)
	\(y=x^4+x^2+1\)
	\(y=\dfrac{x-1}{x+1}\)
	\(y=x^3+5x+13\)

Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?

	$y=x^3-2x^2-1$
	$y=-x^4+2x^2-1$
	$y=x^4-2x^2-1$
	$y=x^4+2x^2+1$

Hàm số nào dưới đây nghịch biến trên tập $\mathbb{R}$?

	$y=3x^3-x$
	$y=-2x^4-x$
	$y=-2x^3+3$
	$y=-x^4+2$

Hàm số nào dưới đây có bảng biến thiên như sau?

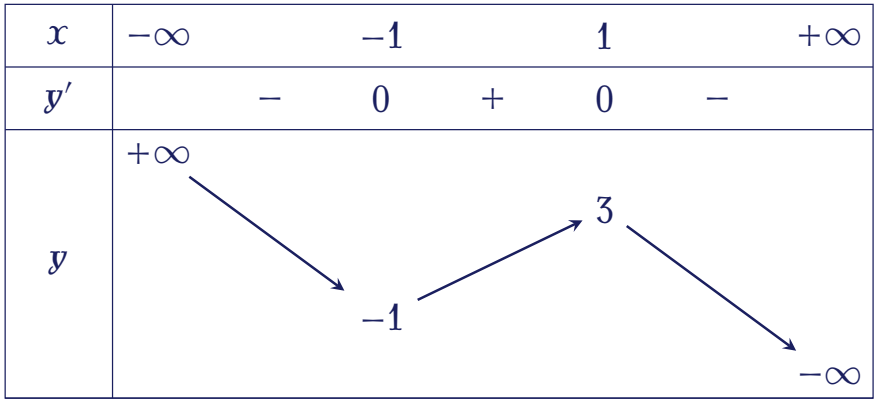
	$y=\dfrac{x+2}{x}$
	$y=-x^3+3x+1$
	$y=x^4-3x^2$
	$y=-2x^2+1$

Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?

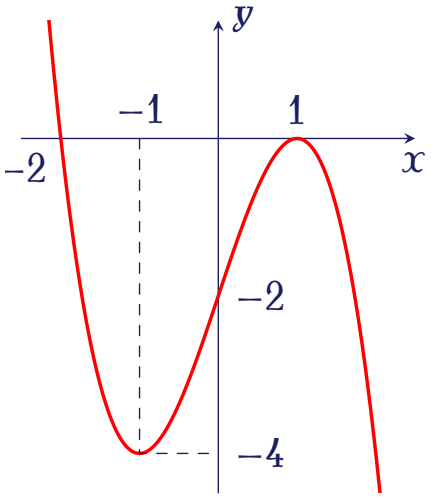
	$y=-x^3+3x-2$
	$y=x^3-3x+2$
	$y=x^4-3x^2-2$
	$y=x^4-3x^2+2$

Tìm tập xác định $\mathscr{D}$ của hàm số $y=\dfrac{3x-1}{2x-2}$.

	$\mathscr{D}=\Bbb{R}$
	$\mathscr{D}=\Bbb{R}\setminus\left\{2\right\}$
	$\mathscr{D}=\left[1;+\infty\right)$
	$\mathscr{D}=\Bbb{R}\setminus\left\{1\right\}$

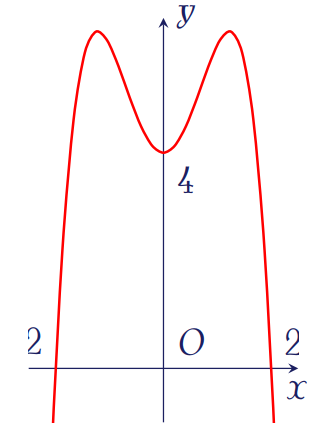
Đồ thị trong hình vẽ bên là của hàm số

	\(y=-x^2+x-4\)
	\(y=x^4-3x^2-4\)
	\(y=-x^3+2x^2+4\)
	\(y=-x^4+3x^2+4\)

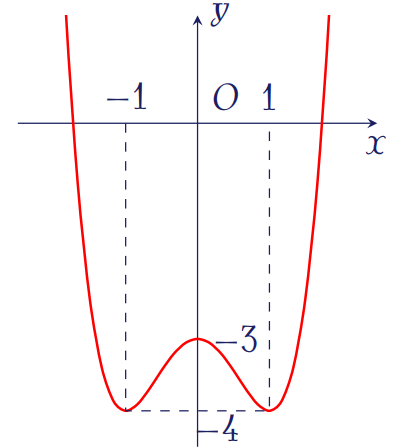
Đường cong trong hình vẽ bên là của hàm số nào sau đây?

	\(y=-x^3+x^2-2\)
	\(y=-x^4+3x^2-2\)
	\(y=x^4-2x^2-3\)
	\(y=-x^2+x-1\)

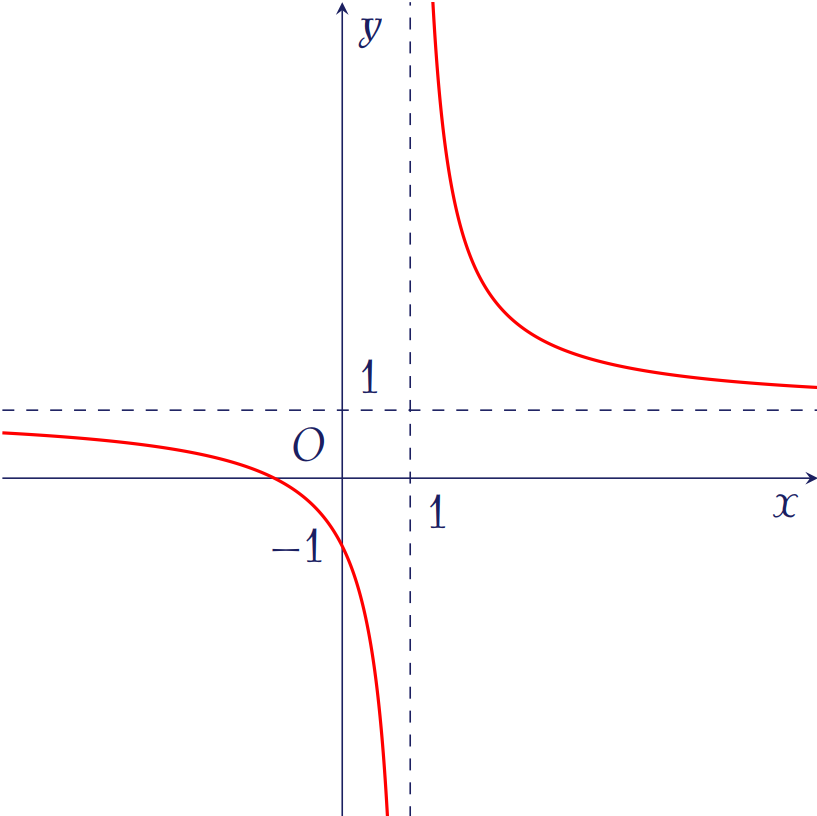
Đường cong trong hình trên là đồ thị của hàm số nào dưới đây?

	\(y=-x^3+3x+1\)
	\(y=\dfrac{x+1}{x-1}\)
	\(y=\dfrac{x-1}{x+1}\)
	\(y=x^3-3x-1\)

Đồ thị hàm số nào sau đây có \(3\) đường tiệm cận?

	\(y=\dfrac{1-2x}{1+x}\)
	\(y=\dfrac{1}{4-x^2}\)
	\(y=\dfrac{x+3}{5x-1}\)
	\(y=\dfrac{x}{x^2-x+9}\)

Đồ thị của hàm số nào dưới đây có tiệm cận đứng?

	\(y=\dfrac{\sqrt{1-x^2}+1}{2019}\)
	\(y=\dfrac{x^2-1}{x-1}\)
	\(y=\dfrac{x^2}{x^2+2018}\)
	\(y=\dfrac{x}{x+12}\)