Đồ thị hàm số nào dưới đây không có đường tiệm cận?
| \(y=\dfrac{x}{x^2+1}\) | |
| \(y=\dfrac{1}{x}\) | |
| \(y=x^4-3x^2+2\) | |
| \(y=\dfrac{2x+1}{2-x}\) |
Đồ thị hàm số nào sau đây có \(3\) đường tiệm cận?
| \(y=\dfrac{1-2x}{1+x}\) | |
| \(y=\dfrac{1}{4-x^2}\) | |
| \(y=\dfrac{x+3}{5x-1}\) | |
| \(y=\dfrac{x}{x^2-x+9}\) |
Đồ thị hàm số \(y=\dfrac{x^2+2x+3}{\sqrt{x^4-3x^2+2}}\) có bao nhiêu đường tiệm cận?
| \(4\) | |
| \(5\) | |
| \(3\) | |
| \(6\) |
Đồ thị hàm số \(y=\dfrac{\sqrt{x+1}}{x^2-1}\) có bao nhiêu đường tiệm cận?
| \(3\) | |
| \(1\) | |
| \(2\) | |
| \(0\) |
Đồ thị hàm số \(y=\dfrac{x+1}{\sqrt{x^2-1}}\) có bao nhiêu đường tiệm cận?
| \(3\) | |
| \(1\) | |
| \(2\) | |
| \(0\) |
Đồ thị của hàm số nào sau đây nhận đường thẳng \(x=2\) làm tiệm cận đứng?
| \(y=\dfrac{1}{x+1}\) | |
| \(y=\dfrac{5x}{2-x}\) | |
| \(y=x-2+\dfrac{1}{x+1}\) | |
| \(y=\dfrac{1}{x+2}\) |
Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{x+1}-1}{x^3-4x}\) lần lượt là
| \(3\) và \(1\) | |
| \(1\) và \(1\) | |
| \(2\) và \(1\) | |
| \(1\) và \(0\) |
Đồ thị hàm số nào sau đây có đúng $1$ đường tiệm cận ngang?
| $y=\dfrac{\sqrt{2-x^2}}{x+3}$ | |
| $y=\dfrac{4x-3}{x^2-2x}$ | |
| $y=\dfrac{\sqrt{x^2+1}}{5x-3}$ | |
| $y=\dfrac{x^2-x}{x+1}$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,\,b,\,c\in\mathbb{R}$) có đồ thị như hình bên.
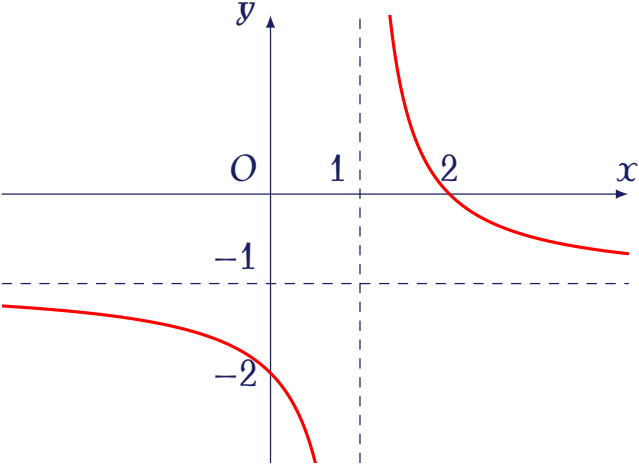
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-1}{x-2}$ có phương trình là
| $x=2$ | |
| $x=-2$ | |
| $x=3$ | |
| $x=\dfrac{1}{2}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x+1}$ là đường thẳng có phương trình
| $y=-1$ | |
| $x=-1$ | |
| $y=2$ | |
| $x=2$ |
Đồ thị hàm số nào sau đây có tiệm cận ngang?
| $y=\dfrac{1-x^2}{x}$ | |
| $y=\dfrac{\sqrt{x^2-1}}{x}$ | |
| $y=\dfrac{x^2-1}{x}$ | |
| $y=\dfrac{\sqrt{1-x^2}}{x}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-3}$ là đường thẳng có phương trình
| $x=\dfrac{1}{2}$ | |
| $x=\dfrac{1}{3}$ | |
| $x=2$ | |
| $x=3$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
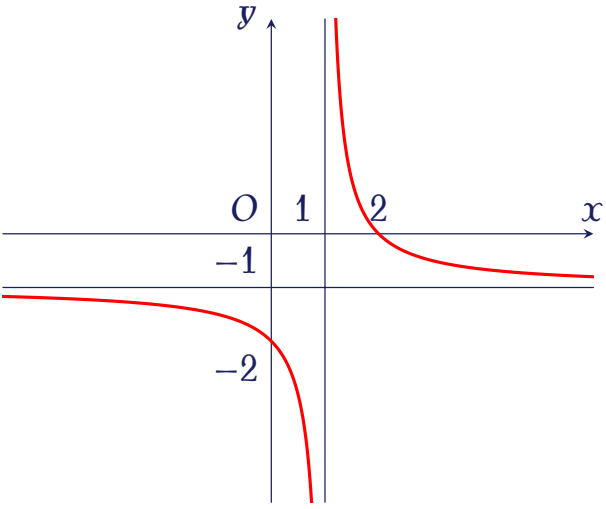
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Cho hàm số $y=\dfrac{x}{x-1}+2$ có đồ thị $\left(\mathscr{C}\right)$ Mệnh đề nào dưới đây đúng?
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=1$ | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=3$ | |
| Đồ thị $\left(\mathscr{C}\right)$ không có tiệm cận | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận đứng $x=2$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-1}$ là đường thẳng có phương trình
| $x=1$ | |
| $x=-1$ | |
| $x=2$ | |
| $x=\dfrac{1}{2}$ |
