Cho $x,\,y$ là các số thực thỏa mãn $(x-3)^2+(y-1)^2=5$. Giá trị nhỏ nhất của biểu thức $P=\dfrac{3y^2+4xy+7x+4y-1}{x+2y+1}$ là
| $2\sqrt{3}$ | |
| $\dfrac{114}{11}$ | |
| $\sqrt{3}$ | |
| $3$ |
Cho $x,\,y$ là hai số thực bất kì thuộc đoạn $[1;3]$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $S=\dfrac{x}{y}+\dfrac{y}{x}$. Tính $M+m$.
| $M+m=\dfrac{10}{3}$ | |
| $M+m=\dfrac{16}{3}$ | |
| $M+m=3$ | |
| $M+m=5$ |
Cho hai số thực $x,\,y$ thay đổi thỏa mãn điều kiện $x^2+y^2=2$. Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=2\big(x^3+y^3\big)-3xy$. Giá trị của $M+m$ bằng
| $-4$ | |
| $-\dfrac{1}{2}$ | |
| $-6$ | |
| $1-4\sqrt{2}$ |
Xét các số thực không âm \(x\) và \(y\) thỏa mãn \(2x+y\cdot4^{x+y-1}\geq3\). Giá trị nhỏ nhất của biểu thức \(P=x^2+y^2+4x+6y\) bằng
| \(\dfrac{33}{4}\) | |
| \(\dfrac{65}{8}\) | |
| \(\dfrac{49}{8}\) | |
| \(\dfrac{57}{8}\) |
Cho \(x,\,y\) là hai số không âm thỏa mãn \(x+y=2\). Tìm giá trị nhỏ nhất của biểu thức $$P=\dfrac{x^3}{3}+x^2+y^2-x+1$$
| \(\dfrac{17}{3}\) | |
| \(5\) | |
| \(\dfrac{115}{3}\) | |
| \(\dfrac{7}{3}\) |
Cho các số dương \(a,\,b,\,c\) thỏa mãn \(abc=8\). Tìm giá trị nhỏ nhất của biểu thức $$P=(a+b)(b+c)(c+a).$$
| \(16\sqrt{2}\) | |
| \(64\) | |
| \(16\) | |
| \(8\) |
Cho biết \(9^x-12^2=0\), tính giá trị của biểu thức $$P=\dfrac{1}{3^{-x-1}}-8\cdot9^{\tfrac{x-1}{2}}+19.$$
| \(31\) | |
| \(23\) | |
| \(22\) | |
| \(15\) |
Cho hai số \(x,\,y\) sao cho \(xy=3\). Giá trị nhỏ nhất của \(A=x^2+y^2\) là
| \(2\) | |
| \(3\) | |
| \(4\) | |
| \(6\) |
Cho ba số \(x,\,y,\,z>0\). Tìm giá trị nhỏ nhất của biểu thức $$S=\dfrac{x+y}{z}+\dfrac{y+z}{x}+\dfrac{z+x}{y}$$
| \(0\) | |
| \(2\) | |
| \(4\) | |
| \(6\) |
Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
Tìm $m$ sao cho bất phương trình $\dfrac{x^2-2x+2}{x-1}\leq m$ có đúng một nghiệm trên khoảng $(1;+\infty)$.
| $m\geq2$ | |
| $m\leq2$ | |
| $m=2$ | |
| $m>2$ |
Tìm giá trị nhỏ nhất \(m\) của hàm số \(f(x)=\dfrac{x^2+32}{4(x-2)}\) trên khoảng \((2;+\infty)\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(f(x)=\dfrac{4}{x}+\dfrac{x}{1-x}\) trên khoảng \((0;1)\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(f(x)=\dfrac{(x+2)(x+8)}{x}\) trên khoảng \((0;+\infty)\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(f(x)=\dfrac{x^2+2x+2}{x+1}\) trên khoảng \((-1;+\infty)\).
Cho hàm số $y=\dfrac{\sin x-\cos x+\sqrt{2}}{\sin x+\cos x+2}$. Giả sử hàm số có giá trị lớn nhất là $M$, giá trị nhỏ nhất là $N$. Khi đó, giá trị của $2M+N$ là
| $4\sqrt{2}$ | |
| $2\sqrt{2}$ | |
| $4$ | |
| $\sqrt{2}$ |
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \((-6;5)\) sao cho phương trình $$2\cos2x+4\sin x-m\sqrt{2}=0$$vô nghiệm?
| \(3\) | |
| \(2\) | |
| \(4\) | |
| \(5\) |
Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).
| \(m\leq3\) | |
| \(m\leq-3\) | |
| \(m\leq5\) | |
| \(m\leq-1\) |
Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(5\)dm, người ta cắt bỏ bốn tam giác bằng nhau \(AMB\), \(BNC\), \(CPD\), \(DQA\).
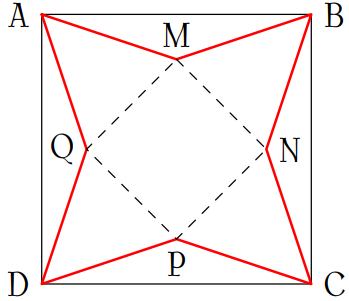
Với phần còn lại, người ta gắp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
| \(\dfrac{3\sqrt{2}}{2}\) | |
| \(\dfrac{5}{2}\) | |
| \(\dfrac{5\sqrt{2}}{2}\) | |
| \(2\sqrt{2}\) |
Tìm giá trị nhỏ nhất \(m\) của hàm số \(f(x)=\dfrac{x^2+32}{4(x-2)}\) trên khoảng \((2;+\infty)\).
| \(m=\dfrac{1}{2}\) | |
| \(m=\dfrac{7}{2}\) | |
| \(m=4\) | |
| \(m=8\) |
