Cho hàm số $y=\dfrac{-x+1}{2x-1}$ có đồ thị $(\mathscr{C})$ và đường thẳng $(d)\colon y=x+m$. Với mọi giá trị thực của $m$ đường thẳng $(d)$ luôn cắt đồ thị $(\mathscr{C})$ tại hai điểm phân biệt $A$ và $B$. Gọi $k_1,\,k_2$ lần lượt là hệ số góc của các tiếp tuyến với $(\mathscr{C})$ tại $A$ và $B$. Giá trị nhỏ nhất của $T=k_1^{2022}+k_2^{2022}$ bằng
| $\dfrac{1}{2}$ | |
| $2$ | |
| $\dfrac{2}{3}$ | |
| $1$ |
Cho hàm số trùng phương $f(x)=ax^4+bx^2+c$ có đồ thị như hình vẽ.
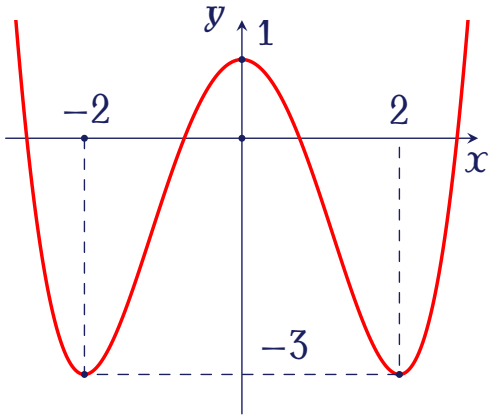
Hỏi đồ thị hàm số $y=\dfrac{2022}{\big[f(x)\big]^2+2f(x)-3}$ có tổng cộng bao nhiêu tiệm cận đứng?
| $4$ | |
| $3$ | |
| $5$ | |
| $2$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
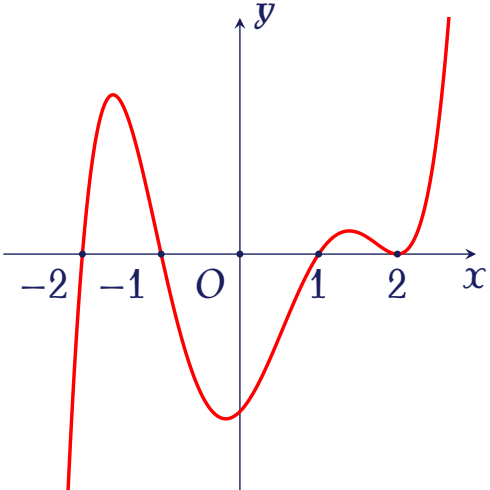
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có bảng xét dấu của $f'(x)$ như sau:
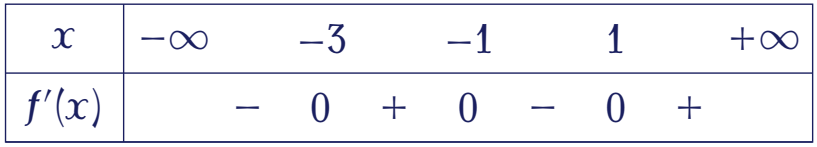
Hàm số $y=f(5-2x)$ đồng biến trên khoảng nào dưới đây?
| $(1;3)$ | |
| $(-\infty;-3)$ | |
| $(3;4)$ | |
| $(4;5)$ |
Cho $a$ và $b$ là hai số thực dương khác $1$ và các hàm số $y=a^x$, $y=b^x$ có đồ thị như hình bên.
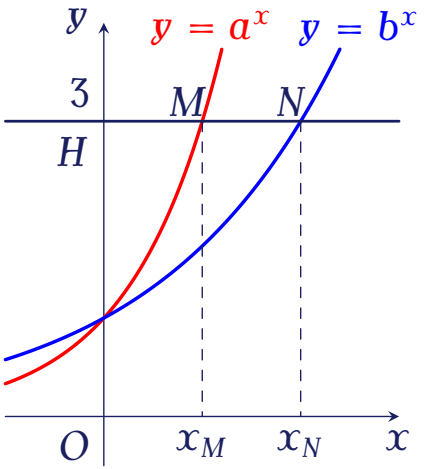
Đường thẳng $y=3$ cắt trục tung, đồ thị hàm số $y=a^x$, đồ thị hàm số $y=b^x$ lần lượt tại $H,\,M,\,N$. Biết rằng $HM=2MN$. Mệnh đề nào sau đây đúng?
| $a^2=b^3$ | |
| $3a=2b$ | |
| $a^3=b^2$ | |
| $2a=b$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong như hình vẽ bên.
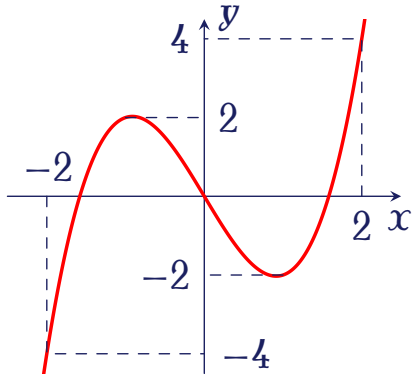
Hỏi phương trình $\big|f(x)-1\big|=1$ có bao nhiêu nghiệm?
| $6$ | |
| $3$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{0\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.
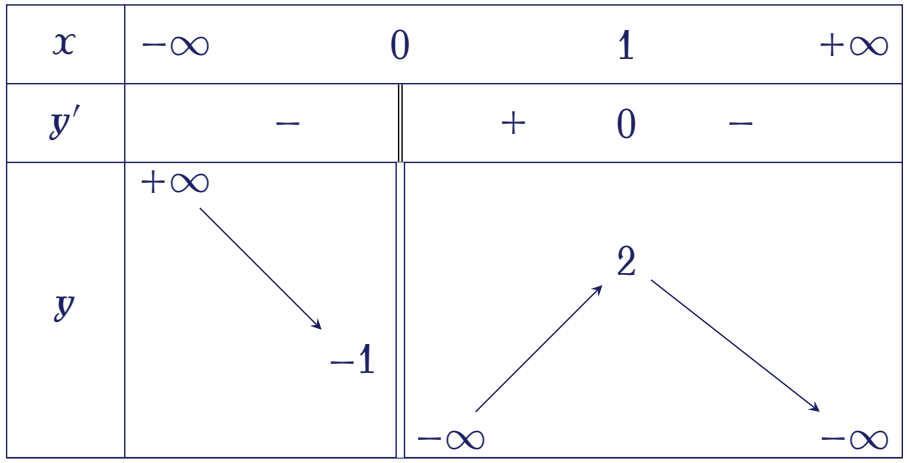
Tập hợp tất cả các giá trị của tham số $m$ sao cho phương trình $f(x)=m$ có ba nghiệm phân biệt là
| $(-\infty;2)$ | |
| $\{-1;2\}$ | |
| $[-1;2]$ | |
| $(-1;2)$ |
Có bao nhiêu giá trị nguyên thuộc đoạn $[-10;10]$ của $m$ để giá trị lớn nhất của hàm số $y=\dfrac{2x+m}{x+1}$ trên đoạn $[-4;-2]$ không lớn hơn $1$?
| $6$ | |
| $7$ | |
| $8$ | |
| $5$ |
Từ một tấm tôn có kích thước $90\text{cm}\times300\text{cm}$, người ta làm một máng thoát nước, mặt cắt ngang của máng là hình thang cân $ABCD$ có đáy lớn $AD$, $AB=BC=CD=30$cm (hình minh họa bên).
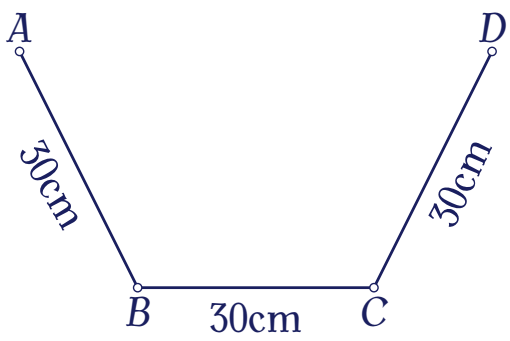
Thể tích lớn nhất của máng bằng
| $40500\sqrt{2}\text{cm}^3$ | |
| $40500\sqrt{5}\text{cm}^3$ | |
| $40500\sqrt{6}\text{cm}^3$ | |
| $202500\sqrt{3}\text{cm}^3$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f'(x)=(x-1)^2(3-x)\big(x^2-x-1\big)$. Hỏi hàm số $f(x)$ có bao nhiêu điểm cực tiểu?
| $3$ | |
| $2$ | |
| $1$ | |
| $0$ |
Giá trị nhỏ nhất của hàm số $f(x)=x^2+\dfrac{2}{x}$ trên đoạn $\left[\dfrac{1}{2};3\right]$ bằng
| $4$ | |
| $2$ | |
| $1$ | |
| $3$ |
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên.
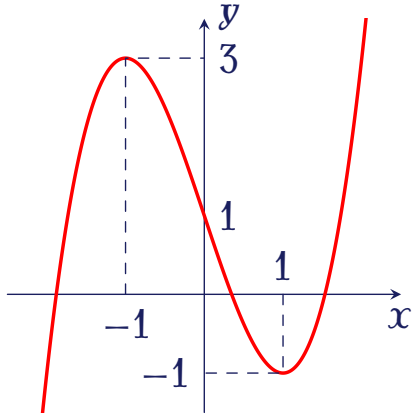
Gọi $M$ là giá trị lớn nhất, $m$ là giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$. Tính $P=M-2m$.
| $P=5$ | |
| $P=3$ | |
| $P=1$ | |
| $P=4$ |
Tập xác định của hàm số $y=(x+2)^{-2022}$ là
| $[-2;+\infty)$ | |
| $(-2;+\infty)$ | |
| $\mathbb{R}\setminus\{-2\}$ | |
| $\mathbb{R}$ |
Trong hình bên là đồ thị các hàm số $y=a^x$ và $y=b^x$.
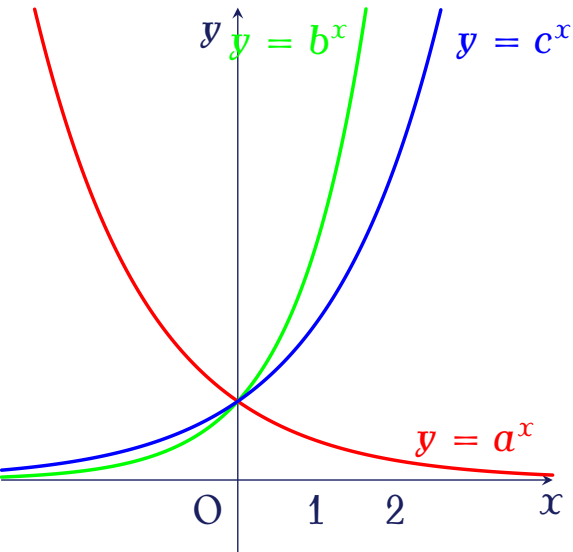
Mệnh đề nào dưới đây là đúng?
| $0< a< 1< b$ | |
| $1< a< b$ | |
| $0< a< b< 1$ | |
| $0< b< 1< a$ |
Tính đạo hàm của hàm số $y=2x^3+x\ln x$ tại điểm $x=1$.
| $6$ | |
| $2$ | |
| $3$ | |
| $7$ |
Hàm số $y=\dfrac{1}{3}x^3+3x^2-7x-\dfrac{20}{3}$ nghịch biến trên khoảng nào trong những khoảng sau đây?
| $(-7;1)$ | |
| $(-7;2)$ | |
| $(-\infty;-7)$ | |
| $(1;+\infty)$ |
Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
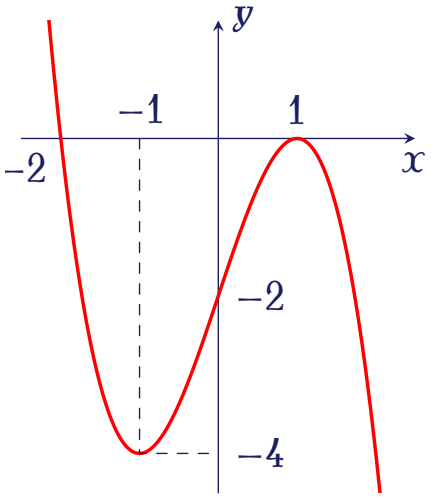
| $y=-x^3+3x-2$ | |
| $y=x^3-3x+2$ | |
| $y=x^4-3x^2-2$ | |
| $y=x^4-3x^2+2$ |
Cho hàm số $f(x)=\big(1-\sqrt[4]{x}\big)\big(1+\sqrt[4]{x}\big)\big(1+\sqrt{x}\big)(1+x)$. Tính $f\left(\dfrac{1}{2^{64}}\right)$.
| $1-\dfrac{1}{2^{128}}$ | |
| $1+\dfrac{1}{2^{64}}$ | |
| $1+\dfrac{1}{2^{128}}$ | |
| $1-\dfrac{1}{2^{64}}$ |
Cho hàm số $y=\dfrac{2x+1}{-x+1}$. Khẳng định nào sau đây đúng?
| Hàm số nghịch biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số đồng biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ | |
| Hàm số đồng biến trên $\mathbb{R}\setminus\{1\}$ | |
| Hàm số nghịch biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ |
Đồ thị hàm số nào sau đây có tiệm cận ngang?
| $y=\dfrac{1-x^2}{x}$ | |
| $y=\dfrac{\sqrt{x^2-1}}{x}$ | |
| $y=\dfrac{x^2-1}{x}$ | |
| $y=\dfrac{\sqrt{1-x^2}}{x}$ |
