Biểu thức $a^{\tfrac{4}{3}}\sqrt{a}$ ($a>0$) viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $a^{\tfrac{11}{6}}$ | |
| $a^{\tfrac{10}{3}}$ | |
| $a^{\tfrac{7}{3}}$ | |
| $a^{\tfrac{5}{6}}$ |
Cho đồ thị của các hàm số $y=a^x$, $y=b^x$, $y=c^x$ như hình bên.
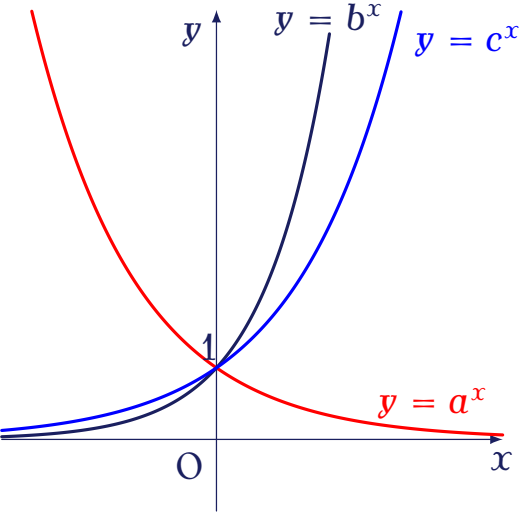
Hỏi trong các số $a,\,b$ và $c$ có bao nhiêu số lớn hơn $1$?
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Tập xác định của hàm số $y=\log_{2022}(2x-1)$ là
| $[0;+\infty)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ | |
| $\left[\dfrac{1}{2};+\infty\right)$ | |
| $(0;+\infty)$ |
Số nghiệm nguyên của bất phương trình $\log_4(2x+3)< 2$ là
| $7$ | |
| $8$ | |
| $9$ | |
| $10$ |
Số $\dfrac{\sqrt[3]{16}}{8}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $2^{\tfrac{13}{3}}$ | |
| $2^{-\tfrac{13}{3}}$ | |
| $2^{\tfrac{5}{3}}$ | |
| $2^{-\tfrac{5}{3}}$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
Nghiệm của phương trình $\log_2(x-1)=3$ là
| $x=10$ | |
| $x=9$ | |
| $x=8$ | |
| $x=7$ |
Tập nghiệm của bất phương trình $3^x\leq81$ là
| $(-\infty;4]$ | |
| $[4;+\infty)$ | |
| $(4;+\infty)$ | |
| $(-\infty;4)$ |
Với $a,\,b,\,c$ là các số thực dương và $a\neq1$ thì $\log_a(b.c)$ bằng
| $\log_ac-\log_ab$ | |
| $\log_ab-\log_ac$ | |
| $\log_ab\cdot\log_ac$ | |
| $\log_ab+\log_ac$ |
Nghiệm của phương trình $2^{x+1}=4$ là
| $x=3$ | |
| $x=1$ | |
| $x=2$ | |
| $x=0$ |
Tập nghiệm của bất phương trình $\log_5x\geq2$ là
| $[10;+\infty)$ | |
| $[0;+\infty)$ | |
| $[32;+\infty)$ | |
| $[25;+\infty)$ |
Gọi $S$ là tập hợp các giá trị nguyên của $y$ sao cho ứng với mỗi $y$, tồn tại duy nhất một giá trị $x\in\left[\dfrac{3}{2};\dfrac{9}{2}\right]$ thỏa mãn $\log_3\big(x^3-6x^2+9x+y\big)=\log_2\big(-x^2+6x-5\big)$. Số phần tử của $S$ là
| $7$ | |
| $1$ | |
| $8$ | |
| $3$ |
Có bao nhiêu số nguyên $x$ thoả mãn $\big(7^x-49\big)\big(\log_3^2x-7\log_3x+6\big)< 0$?
| $728$ | |
| $726$ | |
| $725$ | |
| $729$ |
Với $a$, $b$ là các số thực dương tùy ý thỏa mãn $a\neq1$ và $\log_a b=2$, giá trị của $\log_{a^2}\big(ab^2\big)$ bằng
| 2 | |
| $\dfrac{3}{2}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{5}{2}$ |
Tập nghiệm của bất phương trình $\log_3(2x)\ge\log_32$ là
| $(0;+\infty)$ | |
| $[1;+\infty)$ | |
| $(1;+\infty)$ | |
| $(0;1]$ |
Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Với $b,\,c$ là hai số thực dương tùy ý thỏa mãn $\log_5b\ge\log_5c$, khẳng định nào dưới đây là đúng?
| $b\ge c$ | |
| $b\le c$ | |
| $b>c$ | |
| $b< c$ |
Đạo hàm của hàm số $y=\log_2(x-1)$ là
| $y'=\dfrac{x-1}{\ln2}$ | |
| $y'=\dfrac{1}{\ln2}$ | |
| $y'=\dfrac{1}{(x-1)\ln2}$ | |
| $y'=\dfrac{1}{x-1}$ |
Tập nghiệm của bất phương trình $2^{2x}< 8$ là
| $\left(-\infty;\dfrac{3}{2}\right)$ | |
| $\left(\dfrac{3}{2};+\infty\right)$ | |
| $(-\infty;2)$ | |
| $\left(0;\dfrac{3}{2}\right)$ |
