Cho hàm số $y=f(x)$ liên tục và có bảng biến thiên trên đoạn $[-1;3]$ như hình vẽ.
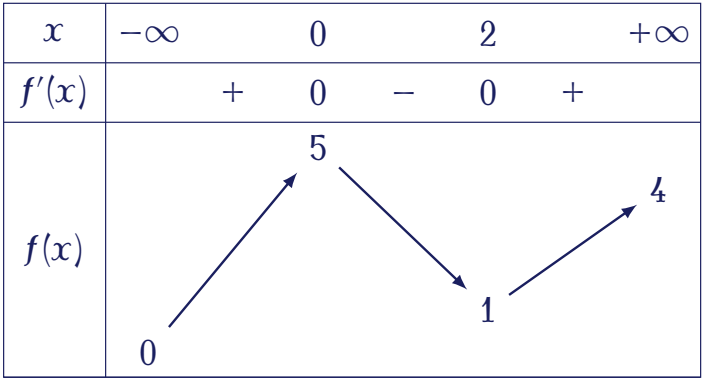
Khẳng định nào sau đây đúng?
| $\max\limits_{[-1;3]}f(x)=f(0)$ | |
| $\max\limits_{[-1;3]}f(x)=f(3)$ | |
| $\max\limits_{[-1;3]}f(x)=f(-1)$ | |
| $\max\limits_{[-1;3]}f(x)=f(2)$ |
Cho hàm số $y=f(x)$ có đồ thị là đường cong như hình vẽ.
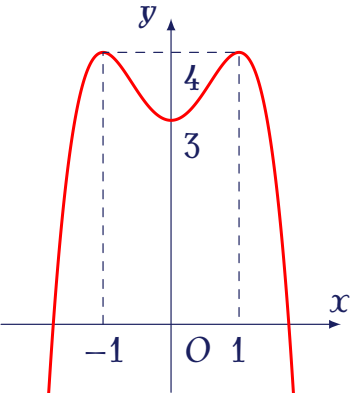
Tọa độ giao điểm của đồ thị đã cho và trục tung là
| $(4;0)$ | |
| $(0;4)$ | |
| $(0;3)$ | |
| $(3;0)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
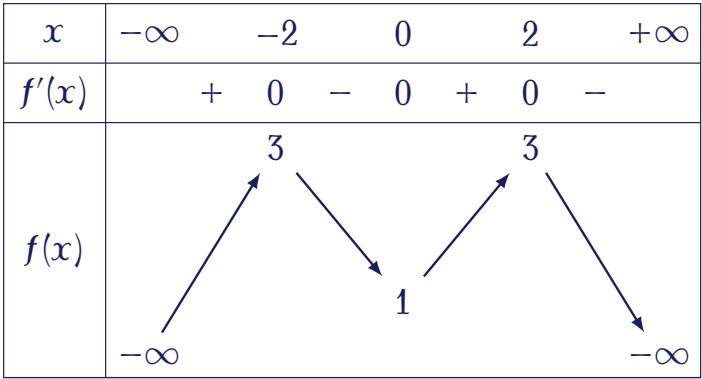
Số điểm cực tiểu của hàm số đã cho là
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Hàm số $y=x^4-2x^2-1$ có bao nhiêu điểm cực trị?
| $2$ | |
| $1$ | |
| $0$ | |
| $3$ |
Khối nón có chiều cao $h=3$cm và bán kính đáy $r=2$cm thì có thể tích bằng bao nhiêu?
| $4\pi\text{ cm}^3$ | |
| $16\pi\text{ cm}^3$ | |
| $\dfrac{4}{3}\pi\text{ cm}^3$ | |
| $4\pi\text{ cm}^2$ |
Với $a>0$ và $a\neq1$, khi đó $\log_a\sqrt[7]{a}$ bằng
| $-\dfrac{1}{7}$ | |
| $\dfrac{1}{7}$ | |
| $-7$ | |
| $7$ |
Đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{3x-4}{x-1}$ là
| $x=3$ | |
| $y=1$ | |
| $x=1$ | |
| $y=3$ |
Một khối trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn đáy lần lượt là $h$, $\ell$, $r$. Khi đó công thức tính diện tích toàn phần của khối trụ là
| $S_{\text{tp}}=\pi r(\ell+r)$ | |
| $S_{\text{tp}}=2\pi r(\ell+r)$ | |
| $S_{\text{tp}}=2\pi r(\ell+2r)$ | |
| $S_{\text{tp}}=\pi r(2\ell+r)$ |
Nghiệm của phương trình $\log_2(3x-2)=0$ là
| $x=2$ | |
| $x=\dfrac{5}{3}$ | |
| $x=\dfrac{4}{3}$ | |
| $x=1$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AB=3$, $AD=4$. Biết đường thẳng $SA$ vuông góc với mặt phẳng đáy và góc tạo bởi đường thẳng $SC$ và mặt phẳng đáy bằng $45^\circ$. Tính bán kính mặt cầu ngoại tiếp hình chóp $S.ABCD$.
| $\dfrac{5\sqrt{2}}{2}$ | |
| $\dfrac{5}{2}$ | |
| $\dfrac{2\sqrt{5}}{3}$ | |
| $\dfrac{5}{3}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Có tât cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Cho số thực $m$ sao cho đường thẳng $x=m$ cắt đồ thị hàm số $y=\log_2x$ tại $A$ và đồ thị hàm số $y=\log_2(x+3)$ tại $B$ thỏa mãn $AB=3$. Khẳng định nào dưới đây đúng?
| $m\in\left(\dfrac{1}{3};\dfrac{1}{2}\right)$ | |
| $m\in\left(0;\dfrac{1}{3}\right)$ | |
| $m\in\left(\dfrac{2}{3};1\right)$ | |
| $m\in\left(\dfrac{1}{2};\dfrac{2}{3}\right)$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\big\{0;1\big\}$ | |
| $\big\{1\big\}$ | |
| $\big\{-1;1\big\}$ | |
| $\big\{0\big\}$ |
Gọi $x_1,\,x_2$ là các nghiệm của phương trình $2\log2+2\log(x+2)=\log x+4\log3$. Tích $x_1x_2$ bằng
| $\dfrac{15}{2}$ | |
| $\dfrac{9}{2}$ | |
| $6$ | |
| $4$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$. Biết diện tích tứ giác $ABCD$ bằng ba lần diện tích tam giác $SAB$. Tính thể tích khối chóp đã cho.
| $\dfrac{a^3\sqrt{7}}{18}$ | |
| $\dfrac{a^3\sqrt{7}}{6}$ | |
| $\dfrac{a^3\sqrt{7}}{3}$ | |
| $\dfrac{a^3\sqrt{7}}{12}$ |
Cho hình trụ có bán kính đáy và chiều cao đều bằng $a$. Gọi $AB,\,CD$ là các dây cung của hai đường tròn đáy sao cho tứ giác $ABCD$ là hình vuông và mặt phẳng $(ABCD)$ không vuông góc với mặt phẳng đáy. Tính độ dài đoạn thẳng $AB$.
| $\dfrac{a\sqrt{5}}{3}$ | |
| $\dfrac{a\sqrt{5}}{2}$ | |
| $\dfrac{a\sqrt{10}}{2}$ | |
| $\dfrac{a\sqrt{10}}{3}$ |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
