Cho hàm số $y=f(x)$ có bảng biến thiên trên đoạn $[-1;3]$ như sau:
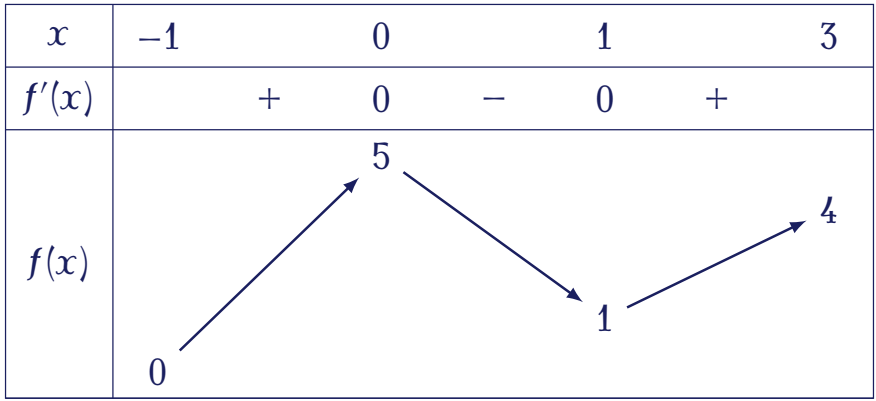
Giá trị lớn nhất của hàm số đã cho trên đoạn $[-1;3]$ bằng
| $1$ | |
| $4$ | |
| $0$ | |
| $5$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ sau:
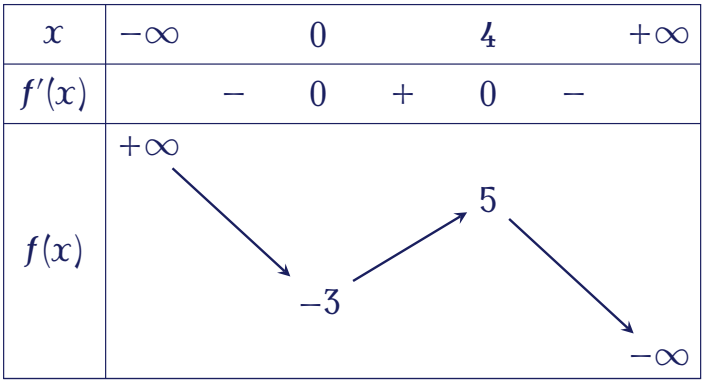
Giá trị lớn nhất của hàm số $g(x)=f\big(4x-x^2\big)+\dfrac{x^3}{3}-3x^2+8x+\dfrac{1}{3}$ trên đoạn $[1;3]$ bằng
| $15$ | |
| $\dfrac{25}{3}$ | |
| $\dfrac{19}{3}$ | |
| $12$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
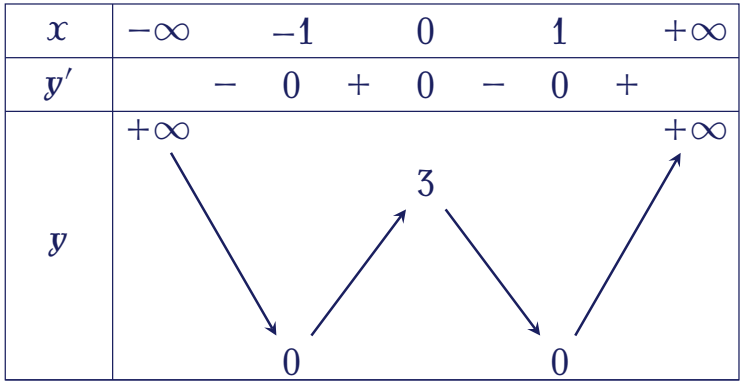
Giá trị lớn nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$ bằng
| $1$ | |
| $3$ | |
| $-1$ | |
| $0$ |
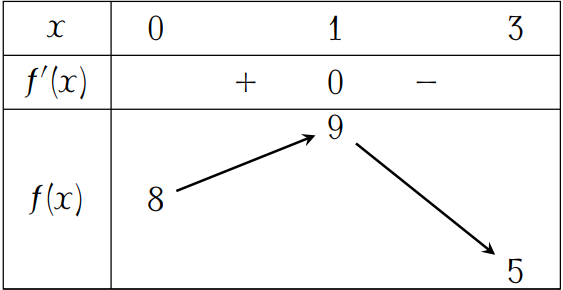
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là
| \(9\) | |
| \(10\) | |
| Vô số | |
| \(0\) |
Hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có bảng biến thiên như sau:

Gọi \(M\) là giá trị lớn nhất của hàm số \(y=f(x)\) trên đoạn \([-1;3]\). Khẳng định nào sau đây là khẳng định đúng?
| \(M=f(0)\) | |
| \(M=f(3)\) | |
| \(M=f(2)\) | |
| \(M=f(-1)\) |
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-3;2]\) và có bảng biến thiên như sau: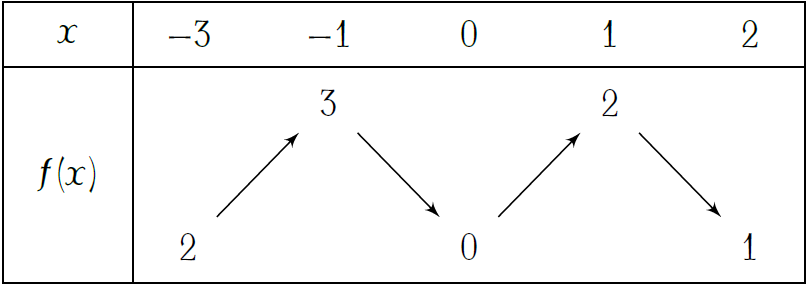
Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(f(x)\) trên đoạn \([-1;2]\). Tính \(M+m\).
| \(3\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
Cho bảng biến thiên của hàm số \(y=f(x)\) như hình.
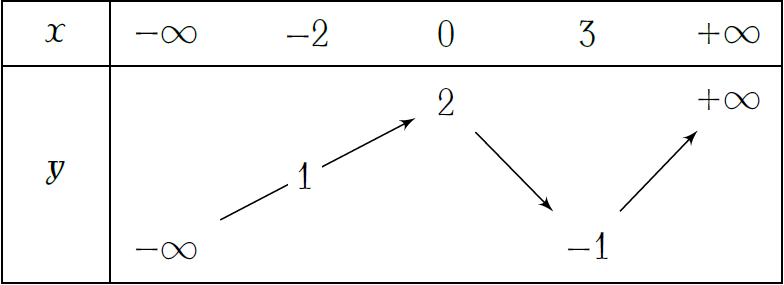
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số trên đoạn \([-2;3]\).
| \(\begin{cases}M=3\\ m=-2\end{cases}\) | |
| \(\begin{cases}M=0\\ m=3\end{cases}\) | |
| \(\begin{cases}M=2\\ m=-1\end{cases}\) | |
| \(\begin{cases}M=1\\ m=-1\end{cases}\) |
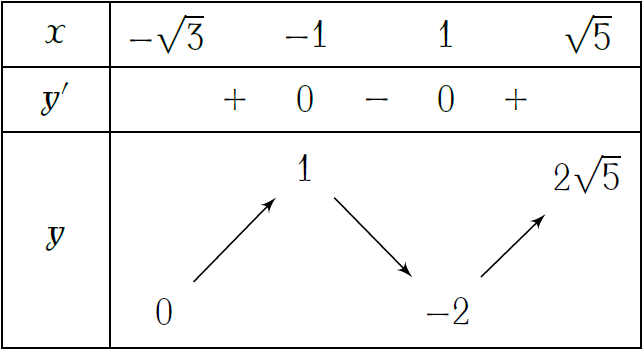
Cho hàm số \(y=f(x)\) xác định trên đoạn \(\left[-\sqrt{3};\sqrt{5}\right]\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=0\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) | |
| \(\max\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\sqrt{5}\) | |
| \(\min\limits_{\left[-\sqrt{3};\sqrt{5}\right]}f(x)=2\) |
Cho hai cây cột có chiều cao lần lượt là $6$m, $15$m và đặt cách nhau $20$m (như hình minh họa).
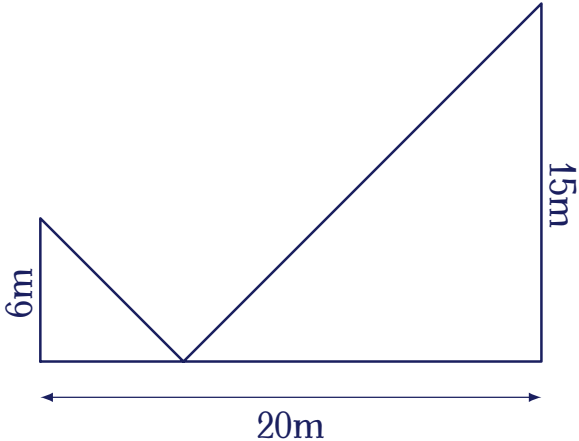
Một sợi dây dài được gắn vào đỉnh của mỗi cột và được đóng cọc xuống đất tại một điểm ở giữa hai cột. Chiều dài sợi dây được sử dụng ít nhất là
| $30$m | |
| $29$m | |
| $31$m | |
| $28$m |
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên.
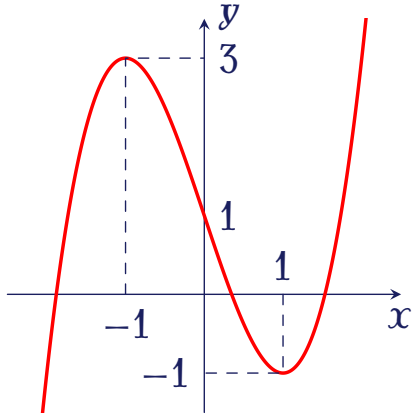
Gọi $M$ là giá trị lớn nhất, $m$ là giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$. Tính $P=M-2m$.
| $P=5$ | |
| $P=3$ | |
| $P=1$ | |
| $P=4$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$, đồ thị của hàm số $y=f'(x)$ như hình vẽ.
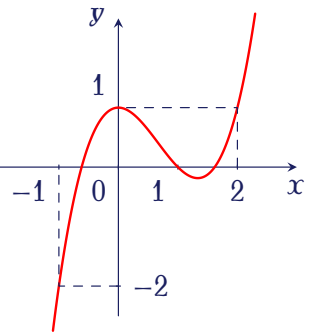
Giá trị lớn nhất của hàm số $g(x)=2f(x)-(x-1)^2$ trên đoạn $[-1;2]$ bằng
| $2f(0)-1$ | |
| $2f(-1)-4$ | |
| $2f(1)$ | |
| $2f(2)-1$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ có đồ thị $y=f'(x)$ cho như hình vẽ.
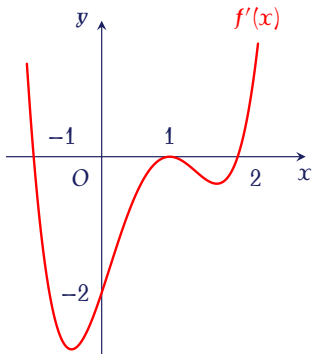
Giá trị nhỏ nhất của hàm số $y=f(x)+\dfrac {1}{3}x^3-x$ trên đoạn $[-1;2]$ bằng
| $f(2)+\dfrac{2}{3}$ | |
| $f(-1)+\dfrac{2}{3}$ | |
| $\dfrac{2}{3}$ | |
| $f(1)-\dfrac{2}{3}$ |
Cho hàm số $f(x)$ có đồ thị $f'(x)$ như hình vẽ.
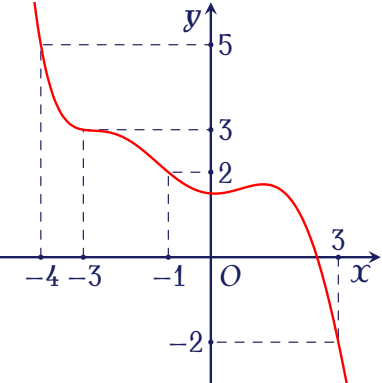
Trên đoạn $[-4;3]$, hàm số $g(x)=2f(x)+(1-x)^2$ đạt giá trị nhỏ nhất tại điểm
| $x_0=-4$ | |
| $x_0=-1$ | |
| $x_0=3$ | |
| $x_0=-3$ |
Cho hàm số $y=f(x)$. Đồ thị của hàm số $y=f'(x)$ như hình vẽ.
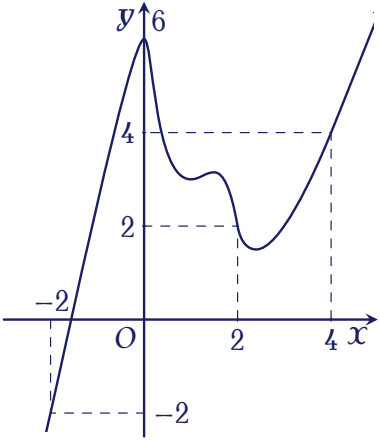
Đặt $h(x)=f(x)-x$. Mệnh đề nào dưới đây đúng?
| $\min\limits_{[-2;2]}h(x)=h(-2)$ | |
| $\max\limits_{[0;4]}h(x)=h(0)$ | |
| $\min\limits_{[-1;2]}h(x)=h(-1)$ | |
| $h(2)< h(4)< h(0)$ |
Cho hàm số $f(x)$, đồ thị của hàm số $y=f'(x)$ là đường cong trong hình bên.
Giá trị lớn nhất của hàm số $g(x)=f(2x)-4x$ trên đoạn $\left[-\dfrac{3}{2};2\right]$ bằng
| $f(0)$ | |
| $f(-3)+6$ | |
| $f(2)-4$ | |
| $f(4)-8$ |
Dựa vào đồ thị của hàm số \(y=\sin x\). Tìm giá trị lớn nhất của hàm số trên \(\left[-\pi;-\dfrac{\pi}{2}\right]\).

| \(1\) | |
| \(0\) | |
| \(-1\) | |
| \(\dfrac{1}{2}\) |
Một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển \(BC=5\) km. Trên bờ biển có một cái kho ở vị trí \(C\) cách \(B\) \(7\) km. Người gác hải đăng có thể chèo đò từ \(A\) đến vị trí \(M\) trên bờ biển với vận tốc \(4\) km/h rồi đi bộ đến \(C\) với vận tốc \(6\) km/h.

Vị trí của điểm \(M\) phải cách \(B\) bao nhiêu km để người gác hải đăng đến \(C\) nhanh nhất?
| \(0\) km | |
| \(\dfrac{14+5\sqrt{5}}{12}\) km | |
| \(2\sqrt{5}\) km | |
| \(7\) km |
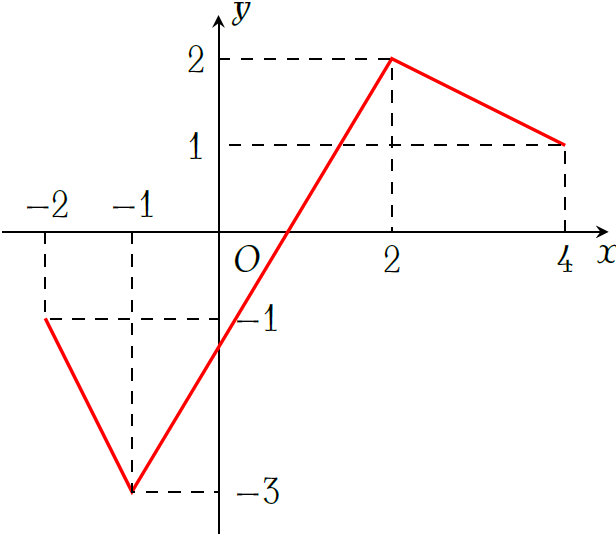
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Tìm \(\max\limits_{[-2;4]}\left|f(x)\right|\).
| \(\left|f(0)\right|\) | |
| \(2\) | |
| \(3\) | |
| \(1\) |
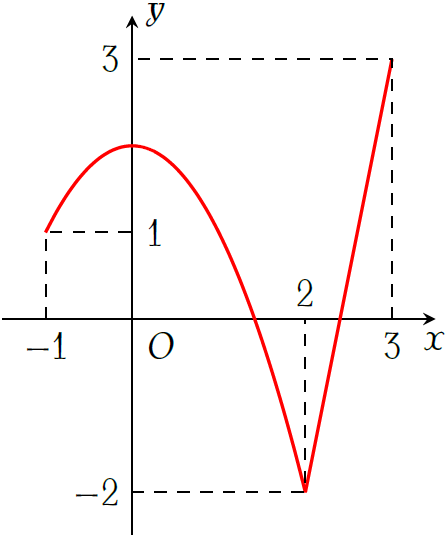
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng
| \(0\) | |
| \(1\) | |
| \(4\) | |
| \(5\) |
Cho hàm số $f(x)=ax^3+cx+d$ ($a\neq0$) có $\min\limits_{x\in(0;+\infty)}f(x)=f(2)$. Tìm giá trị lớn nhất của hàm số trên đoạn $[-3;1]$.
| $24a+d$ | |
| $d-16a$ | |
| $8a-d$ | |
| $d+16a$ |
