Cho hàm số $y=\begin{cases}x^2+ax+b&\text{khi }x\ge2\\ x^3-x^2-8x+10&\text{khi }x<2\end{cases}$. Biết hàm số có đạo hàm tại điểm $x=2$. Giá trị của $a^2+b^2$ bằng
| $20$ | |
| $17$ | |
| $18$ | |
| $25$ |
Cho hàm số $f\left(x\right)=\begin{cases}ax^2+bx+1&\text{khi }x\ge0\\ ax-b-1&\text{khi }x<0\end{cases}$. Khi hàm số $f\left(x\right)$ có đạo hàm tại $x_0=0$, hãy tính $T=a+2b$.
| $T=-4$ | |
| $T=0$ | |
| $T=-6$ | |
| $T=4$ |
Cho hàm số $f\left(x\right)=\begin{cases}\left(x-1\right)^2&\text{khi }x\ge0 \\ -x^2&\text{khi }x<0\end{cases}$ có đạo hàm tại điểm $x_0=0$ bằng
| $f'\left(0\right)=0$ | |
| $f'\left(0\right)=1$ | |
| $f'\left(0\right)=-2$ | |
| Không tồn tại |
Tìm mệnh đề đúng trong số các mệnh đề sau:
| Nếu \(f(x)\) liên tục trên đoạn \([a;b]\) và \(f(a)\cdot f(b)>0\) thì phương trình \(f(x)=0\) có ít nhất một nghiệm trên khoảng \((a;b)\) | |
| Nếu \(f(x)\) liên tục trên đoạn \([a;b]\) và \(f(a)\cdot f(b)<0\) thì phương trình \(f(x)=0\) có ít nhất một nghiệm trên khoảng \((a;b)\) | |
| Nếu \(f(x)\) liên tục trên khoảng \((a;b)\) và \(f(a)\cdot f(b)<0\) thì phương trình \(f(x)=0\) có ít nhất một nghiệm trên khoảng \((a;b)\) | |
| Nếu \(f(x)\) liên tục trên đoạn \([a;b]\) và \(f(a)\cdot f(b)<0\) thì phương trình \(f(x)=0\) có ít nhất một nghiệm trên đoạn \([a;b]\) |
Cho hàm số $$f(x)=\begin{cases}
\dfrac{x^2}{2} &\text{khi }x\leq1\\
ax+b &\text{khi }x>1
\end{cases}$$Tìm tất cả các giá trị của \(a,\,b\) sao cho \(f(x)\) có đạo hàm tại điểm \(x=1\).
| \(a=1,\;b=-\dfrac{1}{2}\) | |
| \(a=\dfrac{1}{2},\;b=\dfrac{1}{2}\) | |
| \(a=\dfrac{1}{2},\;b=-\dfrac{1}{2}\) | |
| \(a=1,\;b=\dfrac{1}{2}\) |
Cho hàm số $$f(x)=\begin{cases}
mx^2+2x+2 &\text{khi }x>0\\
nx+1 &\text{khi }x\leq0
\end{cases}$$Tìm tất cả các giá trị của \(m\) và \(n\) sao cho \(f(x)\) có đạo hàm tại điểm \(x=0\).
| Không tồn tại | |
| \(m=2,\;n\in\mathbb{R}\) | |
| \(n=2,\;m\in\mathbb{R}\) | |
| \(m=n=2\) |
Cho hàm số $$f(x)=\begin{cases}
x^2-1 &\text{khi }x\geq0\\
-x^2 &\text{khi }x<0
\end{cases}$$Khẳng định nào sau đây sai?
| Hàm số không liên tục tại \(x=0\) | |
| Hàm số có đạo hàm tại \(x=2\) | |
| Hàm số liên tục tại \(x=2\) | |
| Hàm số có đạo hàm tại \(x=0\) |
Trong các phát biểu sau, phát biểu nào đúng?
| Nếu hàm số \(y=f(x)\) không liên tục tại \(x_0\) thì nó có đạo hàm tại điểm đó | |
| Nếu hàm số \(y=f(x)\) có đạo hàm tại \(x_0\) thì nó không liên tục tại điểm đó | |
| Nếu hàm số \(y=f(x)\) có đạo hàm tại \(x_0\) thì nó liên tục tại điểm đó | |
| Nếu hàm số \(y=f(x)\) liên tục tại \(x_0\) thì nó có đạo hàm tại điểm đó |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Cho hàm số $f(x)=\ln\big(x^2+1\big)$. Giá trị $f'(2)$ bằng
| $\dfrac{4}{5}$ | |
| $\dfrac{4}{3\ln2}$ | |
| $\dfrac{4}{2\ln5}$ | |
| $2$ |
Đạo hàm của hàm số $y=x^{2023}$ là
| $y'=2023x^{2023}$ | |
| $y'=2022x^{2023}$ | |
| $y'=2023x^{2022}$ | |
| $y'=\dfrac{1}{2023}x^{2022}$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
| $(-\infty;2)$ | |
| $(-\infty;-1)$ | |
| $(-1;2)$ | |
| $(-1;+\infty)$ |
Cho hàm số $y=f(x)$ có $f'(x)$ liên tục trên $\mathbb{R}$ và đồ thị $f'(x)$ như hình bên.
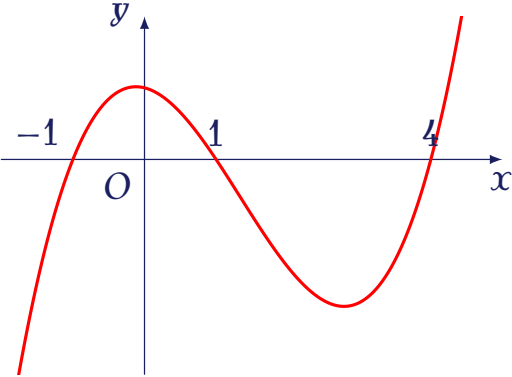
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
| $(-\infty;0)$ | |
| $(-1;1)$ | |
| $(1;4)$ | |
| $(1;+\infty)$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Giá trị nhỏ nhất của hàm số $y=x^3+3x^2-1$ trên đoạn $[-1;1]$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $2$ |
