Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
| ABC là tam giác đều \(\Leftrightarrow\) tam giác ABC cân | |
| ABC là tam giác đều \(\Leftrightarrow\) tam giác ABC cân và có một góc \(60^\circ\) | |
| ABC là tam giác đều \(\Leftrightarrow\) tam giác ABC có ba cạnh bằng nhau | |
| ABC là tam giác đều \(\Leftrightarrow\) tam giác ABC có hai góc \(60^\circ\) |
Trong các câu sau, câu nào là mệnh đề đúng?
| Nếu \(a\geq b\) thì \(a^2\geq b^2\) | |
| Nếu \(a\) chia hết cho \(9\) thì \(a\) chia hết cho \(3\) | |
| Nếu em chăm chỉ thì em thành công | |
| Nếu một tam giác có một góc bằng \(60^\circ\) thì tam giác đó đều |
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
| Nếu số nguyên \(n\) có chữ số tận cùng là \(5\) thì \(n\) chia hết cho \(5\) | |
| Nếu tứ giác \(ABCD\) có hai đường chéo cắt nhau tại trung điểm mỗi đường thì \(ABCD\) là hình bình hành | |
| Nếu tứ giác \(ABCD\) là hình chữ nhật thì \(ABCD\) có hai đường chéo bằng nhau | |
| Nếu tứ giác \(ABCD\) là hình thoi thì \(ABCD\) có hai đường chéo vuông góc với nhau |
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
| Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đó đều là số chẵn | |
| Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đó đều là số chẵn | |
| Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đó đều là số lẻ | |
| Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đó đều là số lẻ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho tam giác đều \(ABC\). Hãy xác định góc quay \(\varphi\) của phép quay tâm \(A\) biến điểm \(B\) thành điểm \(C\).
| \(\varphi=30^\circ\) | |
| \(\varphi=90^\circ\) | |
| \(\varphi=-120^\circ\) | |
| \(\varphi=60^\circ\) hoặc \(\varphi=-60^\circ\) |
Cho tam giác đều tâm \(O\). Với giá trị nào của \(\varphi\) thì phép quay \(\mathrm{Q}_{\left(O,\varphi\right)}\) biến tam giác đều đã cho thành chính nó?
| \(\varphi=\dfrac{\pi}{3}\) | |
| \(\varphi=\dfrac{2\pi}{3}\) | |
| \(\varphi=\dfrac{3\pi}{2}\) | |
| \(\varphi=\dfrac{\pi}{2}\) |
Cho \(x\) là một phần tử của tập hợp \(A\). Xét các mệnh đề sau:
- \(x\in A\)
- \(\{x\}\in A\)
- \(x\subset A\)
- \(\{x\}\subset A\)
Trong các mệnh đề trên, mệnh đề nào đúng?
| I và II | |
| I và III | |
| I và IV | |
| II và IV |
Chọn cụm từ còn thiếu trong định nghĩa sau:
"Phương trình ẩn \(x\) là .............. có dạng \(f(x)=g(x)\), trong đó \(f(x)\) và \(g(x)\) là những biểu thức của \(x\)."
| Biểu thức | |
| Hàm số | |
| Mệnh đề | |
| Mệnh đề chứa biến |
Phát biểu sau đúng hay sai:
"Bất đẳng thức là mệnh đề chứa biến có dạng \(a< b\) hoặc \(a>b\) hoặc \(a\leq b\) hoặc \(a\geq b\)."
| Đúng | |
| Sai |
Mệnh đề nào sau đây tương đương với mệnh đề \(A\neq\varnothing\)?
| \(\forall x,\,x\in A\) | |
| \(\exists x,\,x\in A\) | |
| \(\exists x,\,x\notin A\) | |
| \(\forall x,\,x\subset A\) |
Thiết diện qua trục của một hình nón tròn xoay là tam giác đều có diện tích bằng $a^2\sqrt{3}$. Tính thể tích $V$ của khối nón đã cho.
| $V=\dfrac{\pi a^3\sqrt{3}}{3}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{2}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{6}$ | |
| $V=\dfrac{\pi a^3\sqrt{6}}{6}$ |
Cho hình vuông $ABCD$ tâm $O$ (như hình).
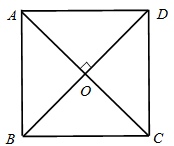
Xác định ảnh của tam giác $OBC$ qua phép quay tâm $O$ góc quay $\dfrac{\pi}{2}$?
| $\triangle OCB$ | |
| $\triangle OAD$ | |
| $\triangle OAB$ | |
| $\triangle OCD$ |
Cho hình vuông $ABCD$ tâm $O$. Gọi $M,\,N,\,P,\,Q$ lần lượt là trung điểm của các cạnh $AB$, $BC$, $CD$, $DA$.
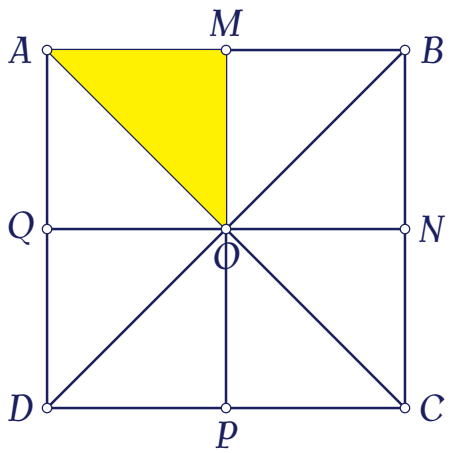
Ảnh của tam giác $OAM$ qua phép quay tâm $O$ góc $90^\circ$ là
| $\triangle ODQ$ | |
| $\triangle OBN$ | |
| $\triangle OAQ$ | |
| $\triangle OCN$ |
Cho hàm số $y=\dfrac{9}{8}x^4+3(m-3)x^2+4m+2022$ với $m$ là tham số thực. Tìm giá trị của $m$ để đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều.
| $m=-2$ | |
| $m=2$ | |
| $m=3$ | |
| $m=2022$ |
Cắt hình nón $(X)$ bởi mặt phẳng đi qua đỉnh và tạo với mặt chứa đáy góc $60^\circ$, ta được thiết diện là tam giác đều cạnh $4a$. Diện tích xung quanh của $(X)$ bằng
| $8\sqrt{7}\pi a^2$ | |
| $4\sqrt{13}\pi a^2$ | |
| $8\sqrt{13}\pi a^2$ | |
| $4\sqrt{7}\pi a^2$ |
Tam giác $HPS$ đều, cạnh $PS=a\sqrt{2}$. $S_{HPS}$ bằng
| $a^2\dfrac{\sqrt{3}}{4}$ | |
| $a^2\dfrac{\sqrt{6}}{4}$ | |
| $a^2\dfrac{\sqrt{3}}{2}$ | |
| $a^2\dfrac{\sqrt{6}}{2}$ |
Tam giác $ABC$ vuông cân tại $B$, có cạnh $AB=2a$. Phát biểu nào sau đây không đúng?
| $S=\dfrac{a^2}{2}$ | |
| $\widehat{A}=\widehat{C}=45^\circ$ | |
| $AB=BC=2a$ | |
| $S=2a^2$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều và $SA$ vuông góc với mặt đáy. Tam giác $SBC$ là
| Tam giác đều | |
| Tam giác cân | |
| Tam giác vuông cân | |
| Tam giác vuông |
Tổng ba góc trong tam giác luôn bằng
| $45^\circ$ | |
| $90^\circ$ | |
| $180^\circ$ | |
| $360^\circ$ |
