Trong các hàm số $y=\sin x$, $y=\cos x$, $y=\tan x$, $y=\cot x$, có bao nhiêu hàm số tuần hoàn với chu kì $\pi$?
| $2$ | |
| $3$ | |
| $4$ | |
| $1$ |
Trong các hàm số sau, hàm số nào là hàm số chẵn?
| $y=\sin x$ | |
| $y=\cos x$ | |
| $y=\tan x$ | |
| $y=\cot x$ |
Tập xác định của hàm số $y=\cos x$ là tập hợp nào trong các tập hợp dưới đây?
| $\mathbb{R}$ | |
| $\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{k\pi,\,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,\,k\in\mathbb{Z}\right\}$ |
Tìm tập giá trị của hàm số $y=\cot x$.
| $\mathbb{R}$ | |
| $\left[-1;1\right]$ | |
| $\mathbb{R}\setminus\left\{k\pi,\,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,\,k\in\mathbb{Z}\right\}$ |
Tìm tập xác định của hàm số $y=\cot\dfrac{x}{2}$.
| $\mathbb{R}\setminus\left\{k\pi,\,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{k2\pi,\,k\in\mathbb{Z}\right\}$ | |
| $\mathbb{R}\setminus\left\{\pi+k2\pi,\,k\in\mathbb{Z}\right\}$ |
Gọi $M$ và $m$ lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=2\cos2x+3$. Tính tổng $M+m$.
| $8$ | |
| $6$ | |
| $7$ | |
| $3$ |
Trong các hàm số sau, hàm số nào là hàm số chẵn?
| $y=\sin2x$ | |
| $y=x\cos x$ | |
| $y=\cos x\cdot\cot x$ | |
| $y=\cot x\cdot\sin x$ |
Tìm nghiệm của phương trình $\cos x=1$.
| $x=\dfrac{\pi}{2}+k\pi\,(k\in\mathbb{Z})$ | |
| $x=k2\pi\,(k\in\mathbb{Z})$ | |
| $x=k\pi\,(k\in\mathbb{Z})$ | |
| $x=\pi+k\pi\,(k\in\mathbb{Z})$ |
Phương trình $\sin x=\sin\alpha$ có nghiệm là
| $\left[\begin{array}{l}x=\alpha+k\pi\\ x=\pi-\alpha+k\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k2\pi\\ x=-\alpha+k2\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k\pi\\ x=-\alpha+k\pi\end{array}\right.$ | |
| $\left[\begin{array}{l}x=\alpha+k2\pi\\ x=\pi-\alpha+k2\pi\end{array}\right.$ |
Nghiệm của phương trình $\cos x=\dfrac{\sqrt{2}}{2}$ là
| $x=\pm\dfrac{\pi}{4}+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=\pm\dfrac{\pi}{6}+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=\pm\dfrac{\pi}{3}+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=\pm\dfrac{\pi}{3}+k\pi,\,k\in\mathbb{Z}$ |
Nghiệm của phương trình $\tan x=\tan\alpha$ là
| $x=\alpha+k3\pi,\,k\in\mathbb{Z}$ | |
| $x=\alpha+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=\alpha$ | |
| $x=\alpha+k\pi,\,k\in\mathbb{Z}$ |
Nghiệm của phương trình $\cot x=\cot\dfrac{\pi}{3}$ là
| $x=\pm \dfrac{\pi}{3}+k\pi\,(k\in\mathbb{Z})$ | |
| $x=\dfrac{\pi}{6}+k2\pi\,(k\in\mathbb{Z})$ | |
| $x=\dfrac{\pi}{3}+k\pi\,(k\in\mathbb{Z}).$ | |
| $x=\dfrac{\pi}{3}+k2\pi\,(k\in\mathbb{Z})$ |
Giải phương trình $\cot x=-\sqrt{3}$.
| $x=-\dfrac{\pi}{6}+k2\pi,\,k\in\mathbb{Z}$ | |
| $x=-\dfrac{\pi}{3}+k\pi,\,k\in\mathbb{Z}$ | |
| $x=\dfrac{\pi}{3}+k\pi,\,k\in\mathbb{Z}$ | |
| $x=-\dfrac{\pi}{6}+k\pi,\,k\in\mathbb{Z}$ |
Giải phương trình $\sin\big(x-10^\circ\big)=\dfrac{\sqrt{3}}{2}$.
| $\left[\begin{array}{l}x=70^\circ+k360^\circ\\ x=-70^\circ+k360^\circ\end{array}\right.$ | |
| $\left[\begin{array}{l}x=70^\circ+k360^\circ\\ x=130^\circ+k360^\circ\end{array}\right.$ | |
| $\left[\begin{array}{l}x=70^\circ+k360^\circ\\ x=130^\circ+k180^\circ\end{array}\right.$ | |
| $\left[\begin{array}{l}x=60^\circ+k360^\circ\\ x=120^\circ+k360^\circ\end{array}\right.$ |
Tìm tất cả các giá trị thực của m để phương trình $\sin x=m$ vô nghiệm?
| $\left[\begin{array}{l}m< -1\\ m>1\end{array}\right.$ | |
| $m< -1$ | |
| $-1\le m\le 1$ | |
| $m>1$ |
Phương trình nào sau đây vô nghiệm?
| $5\sin x-1=0$ | |
| $\cot x+2=0$ | |
| $3\tan x-1=0$ | |
| $\cos x-3=0$ |
Đặt $t=\sin x$ với điều kiện $-1\le t\le 1$, phương trình $-\sin^2x-4\sin x+3=0$ trở thành phương trình
| $t^2+4t-3=0$ | |
| $t^2+4t+3=0$ | |
| $-t^2-4t-3=0$ | |
| $-t^2-4t=0$ |
Giải phương trình $\sin^2x+3\sin x-4=0$.
| $x=k2\pi,\,k\in\mathbb{Z}$ | |
| $x=0$ | |
| $x=\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}$ | |
| Vô nghiệm |
Phương trình $\sin x-\sqrt{3}\cos x=1$ tương đương với phương trình nào sau đây?
| $\sin\left(x-\dfrac{\pi}{3}\right)=1$ | |
| $\sin\left(x+\dfrac{\pi}{6}\right)=\dfrac{1}{2}$ | |
| $\sin\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}$ | |
| $\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}$ |
Trong mặt phẳng $Oxy$, cho điểm $M'(x';y')$ là ảnh của điểm $M(x;y)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(a;b)$. Tìm mệnh đề đúng?
| $\begin{cases}x'=x+b\\ y'=y+a\end{cases}$ | |
| $\begin{cases}x'=a-x\\ y'=b-y\end{cases}$ | |
| $\begin{cases}x'=x+a\\ y'=y+b\end{cases}$ | |
| $\begin{cases}x'=x-a\\ y'=y-b\end{cases}$ |
Cho hình chữ nhật $MNPQ$. Tìm ảnh của điểm $Q$ qua phép tịnh biến theo vectơ $\overrightarrow{MN}$.
| Điểm $M$ | |
| Điểm $N$ | |
| Điểm $Q$ | |
| Điểm $P$ |
Trong mặt phẳng $Oxy$, cho điểm $M(1;-3)$. Ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;-2)$ là
| $M’(2;5)$ | |
| $M’(2;-5)$ | |
| $M’(0;-1)$ | |
| $M’(0;-5)$ |
Trong măt phẳng $Oxy$, cho đường thẳng $d$ có phương trình $3x+2y-6=0$. Ảnh của đường thẳng $d$ qua phép tịnh tiến theo $\overrightarrow{v}=(-1;3)$ là đường thẳng $d’$ có phương trình
| $3x+2y-12=0$ | |
| $2x+3y-3=0$ | |
| $2x+3y+1=0$ | |
| $3x+2y-9=0$ |
Cho phép quay $\mathrm{Q}_{(O,\varphi)}$ biến điểm $M$ thành $M'$. Khẳng định nào sau đây là khẳng định đúng?
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\left(OM,OM'\right)=\varphi$ | |
| $OM=OM'$ và $\left(OM,OM'\right)=\varphi$ | |
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\widehat{MOM'}=\varphi$ | |
| $OM=OM'$ và $\widehat{MOM'}=\varphi$ |
Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là
| $A’(0;-1)$ | |
| $A’(-1;0)$ | |
| $A’(0;1)$ | |
| $A’(1;1)$ |
Phép quay $\mathrm{Q}_{(O,\varphi)}$ biến đường tròn $(\mathscr{C})$ có bán kính $R$ thành đường tròn $(\mathscr{C}')$ có bán kính $R'$. Khẳng định nào sau đây đúng?
| $R'=3R$ | |
| $R'=-3R$ | |
| $R'=\dfrac{1}{3}R$ | |
| $R'=R$ |
Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ
| $(-5;-3)$ | |
| $(5;-3)$ | |
| $(5;3)$ | |
| $(-5;3)$ |
Cho hình vuông $ABCD$ tâm $O$ (như hình).
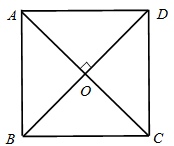
Xác định ảnh của tam giác $OBC$ qua phép quay tâm $O$ góc quay $\dfrac{\pi}{2}$?
| $\triangle OCB$ | |
| $\triangle OAD$ | |
| $\triangle OAB$ | |
| $\triangle OCD$ |
Tìm tập xác định của hàm số $y=\cot\left(x+\dfrac{\pi}{3}\right)$.
Giải các phương trình lượng giác sau:
- $\sin3x+\cos3x=\sqrt{2}\cos2x$
- $(2\sin x-\cos x)(1+\cos x)=\sin^2x$
Trong mặt phẳng $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon(x+3)^2+(y-1)^2=5$ và $\overrightarrow{v}=(2;1)$. Viết phương trình đường tròn $(\mathscr{C}’)$ là ảnh của $(\mathscr{C})$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}$.
