Điểm nào sau đây thuộc đồ thị hàm số $y=\dfrac{2x+1}{x+1}$?
| $M(0;1)$ | |
| $N(-1;0)$ | |
| $P(2;5)$ | |
| $Q(1;0)$ |
Điểm nào dưới đây thuộc đồ thị của hàm số $y=x^4+x^2-2$?
| Điểm $P(-1;-1)$ | |
| Điểm $N(-1;-2)$ | |
| Điểm $M(-1;0)$ | |
| Điểm $Q(-1;1)$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=2|x-1|+3|x|-2$?
| $A(2;6)$ | |
| $B(1;-1)$ | |
| $C(-2;-10)$ | |
| Cả ba điểm $A,\,B,\,C$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=\dfrac{\sqrt{x^2-4x+4}}{x}$?
| $A(2;0)$ | |
| $B\left(3;\dfrac{1}{3}\right)$ | |
| $C(1;-1)$ | |
| $D(-1;-3)$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=x^4-2x^2-1$?
| $A(-1;2)$ | |
| $B(2;7)$ | |
| $C(0;-1)$ | |
| $D(1;-2)$ |
Đỉnh của parabol $\left(P\right)\colon y=3x^2-2x+1$ là
| $I\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$ | |
| $J\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $K\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $L\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=\dfrac{1}{x-1}$?
| $M\left(1;1\right)$ | |
| $N\left(2;1\right)$ | |
| $P\left(2;0\right)$ | |
| $Q\left(0;-2\right)$ |
Phương trình tiếp tuyến của đồ thị hàm số \(y=\dfrac{x-1}{x+1}\) tại điểm \(C(-2;3)\) là
| \(y=-2x+7\) | |
| \(y=2x+7\) | |
| \(y=2x+1\) | |
| \(y=-2x-1\) |
Đường thẳng nào sau đây tiếp xúc với đường cong \(\left(\mathscr{C}\right)\colon y=x^3-2x^2+1\) tại điểm \(A(3;10)\)?
| \(y=15x-35\) | |
| \(y=-15x+55\) | |
| \(y=3x+1\) | |
| \(y=-3x+19\) |
Phương trình tiếp tuyến của đồ thị hàm số \(y=x^3-3x^2-x+3\) tại điểm \(M(1;0)\) là
| \(y=1-x\) | |
| \(y=-4x-4\) | |
| \(y=-4x+4\) | |
| \(y=1-4x\) |
Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y=x^3+5x^2-mx+3\) đi qua điểm \(A(-1;9)\)?
| \(m=\dfrac{2}{3}\) | |
| \(m=-\dfrac{2}{3}\) | |
| \(m=2\) | |
| \(m=-\dfrac{3}{2}\) |
Tìm tọa độ giao điểm \(M\) của đồ thị hàm số \(y=\dfrac{2x-1}{x+2}\) với trục tung.
| \(M\left(\dfrac{1}{2};0\right)\) | |
| \(M\left(0;2\right)\) | |
| \(M\left(0;-\dfrac{1}{2}\right)\) | |
| \(M\left(-\dfrac{1}{2};0\right)\) |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Cho hàm số $f(x)=ax^3+cx+d$ ($a\neq0$) có $\min\limits_{x\in(0;+\infty)}f(x)=f(2)$. Tìm giá trị lớn nhất của hàm số trên đoạn $[-3;1]$.
| $24a+d$ | |
| $d-16a$ | |
| $8a-d$ | |
| $d+16a$ |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\ln\big(x^2-2x+m+1\big)$ có tập xác định là $\mathbb{R}$.
| $m=0$ | |
| $m< -1$ hoặc $m>0$ | |
| $m>0$ | |
| $0< m< 3$ |
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\dfrac{3}{4}x^4-(m-1)x^2-\dfrac{1}{4x^4}$ đồng biến trên khoảng $(0;+\infty)$?
| $4$ | |
| $2$ | |
| $1$ | |
| $3$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình vẽ bên.
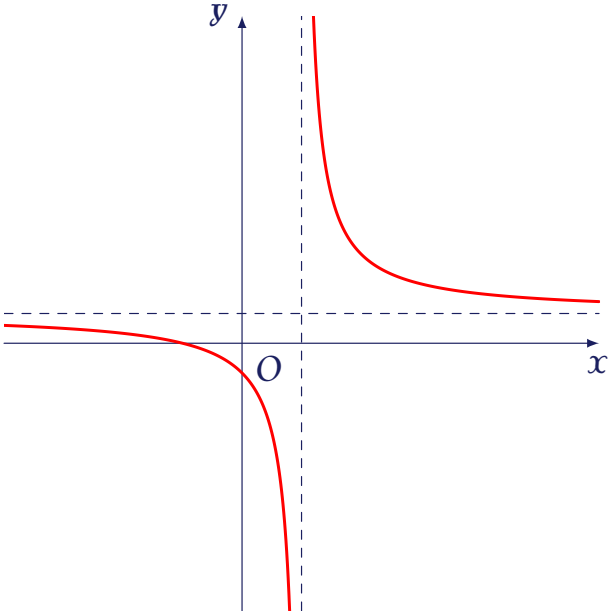
Kết luận nào sau đây đúng?
| $ad>0$, $bc< 0$ | |
| $ad< 0$, $bc>0$ | |
| $ad< 0$, $bc< 0$ | |
| $ad>0$, $bc>0$ |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong như hình vẽ bên dưới.
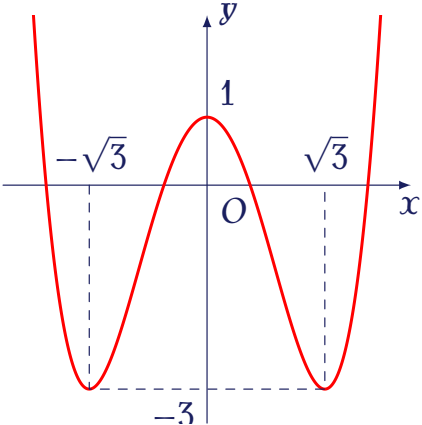
Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình $f(x)=m$ có bốn nghiệm thực phân biệt?
| $3$ | |
| $2$ | |
| $4$ | |
| $5$ |
Hàm số $y=\dfrac{1}{3}x^3-mx^2+\big(m^2-m-1\big)x+m^3$ đạt cực đại tại điểm $x=1$ thì giá trị của tham số $m$ bằng
| $\left[\begin{array}{l}m=0\\ m=3\end{array}\right.$ | |
| $m=0$ | |
| $m=-3$ | |
| $m=3$ |
Kí hiệu $M$ và $m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y=x^2+\sqrt{4-x^2}$. Khi đó $M+m$ bằng
| $\dfrac{25}{4}$ | |
| $\dfrac{15}{4}$ | |
| $4$ | |
| $\dfrac{1}{4}$ |
