Cho hàm số $f(x)$ liên tục trên $(0;+\infty)$. Biết $\dfrac{1}{x^2}$ là một nguyên hàm của hàm số $y=f'(x)\ln x$ và $f(2)=\dfrac{1}{\ln2}$. Khi đó $\displaystyle\displaystyle\int\limits_{1}^{2}\dfrac{f(x)}{x}\mathrm{\,d}x$ bằng
| $-\dfrac{7}{4}$ | |
| $\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}$ | |
| $\dfrac{7}{4}$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) thỏa mãn $z-4=(1+i)|z|-(4+3z)i$. Giá trị của biểu thức $P=a-3b$ bằng
| $P=-2$ | |
| $P=6$ | |
| $P=2$ | |
| $P=-6$ |
Trong không gian $Oxyz$, cho mặt phẳng $(P)\colon ax+by+cz+d=0$ (với $abc>0$) đi qua hai điểm $A(1;0;0)$, $B(0;1;0)$. Biết $\mathrm{d}\big(O,(P)\big)=\dfrac{2}{3}$ và điểm $C(-3;1;0)$. Tính $\mathrm{d}\big(C,(P)\big)$.
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Trong không gian $Oxyz$, cho đường thẳng $d\colon\dfrac{x-1}{1}=\dfrac{y-1}{2}=\dfrac{z-2}{-1}$ và mặt phẳng $(P)\colon2x+y+2z-1=0$. Gọi $d'$ là hình chiếu của đường thẳng $(d)$ lên mặt phẳng $(P)$, vectơ chỉ phương của đường thẳng $d'$ là
| $\overrightarrow{u_2}=(5;-4;-3)$ | |
| $\overrightarrow{u_1}=(5;16;-13)$ | |
| $\overrightarrow{u_3}=(5;-16;-13)$ | |
| $\overrightarrow{u_2}=(5;16;13)$ |
Cho $F(x)=\dfrac{1}{2x^2}$ là một nguyên hàm của hàm số $\dfrac{f(x)}{x}$. Tìm nguyên hàm của hàm số $f'(x)\ln x$.
| $\displaystyle\displaystyle\int f'(x)\ln x\mathrm{\,d}x=-\left(\dfrac{\ln x}{x^2}+\dfrac{1}{x^2}\right)+C$ | |
| $\displaystyle\displaystyle\int f'(x)\ln x\mathrm{\,d}x=\dfrac{\ln x}{x^2}+\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int f'(x)\ln x\mathrm{\,d}x=-\left(\dfrac{\ln x}{x^2}+\dfrac{1}{2x^2}\right)+C$ | |
| $\displaystyle\displaystyle\int f'(x)\ln x\mathrm{\,d}x=\dfrac{\ln x}{x^2}+\dfrac{1}{2x^2}+C$ |
Biết số phức $z$ thỏa mãn $\big|\overline{z}-3-2i\big|=\sqrt{5}$ và tập hợp các điểm biểu diễn số phức $w=(1-i)z+2$ là một đường tròn. Xác định tâm $I$ và bán kính của đường tròn đó.
| $I(-3;-5)$, $R=\sqrt{5}$ | |
| $I(3;-5)$, $R=\sqrt{10}$ | |
| $I(-3;5)$, $R=\sqrt{10}$ | |
| $I(3;5)$, $R=10$ |
Biết $I=\displaystyle\displaystyle\int\limits_{1}^{2}\dfrac{\mathrm{d}x}{(x+1)\sqrt{x}+x\sqrt{x+1}}=\sqrt{a}-\sqrt{b}-c$ với $a,\,b,\,c$ là các số nguyên dương. Tính $P=a+b+c$.
| $P=18$ | |
| $P=12$ | |
| $P=24$ | |
| $P=46$ |
Trong không gian $Oxyz$, cho $M(1;2;1)$. Viết phương trình mặt phẳng $(P)$ qua $M$ cắt các trục $Ox$, $Oy$, $Oz$ lần lượt tại $A,\,B,\,C$ sao cho $\dfrac{1}{OA^2}+\dfrac{1}{OB^2}+\dfrac{1}{OC^2}$ đạt giá trị nhỏ nhất.
| $(P)\colon\dfrac{x}{1}+\dfrac{y}{2}+\dfrac{z}{1}=1$ | |
| $(P)\colon x+y+z-4=0$ | |
| $(P)\colon x+2y+3z-8=0$ | |
| $(P)\colon x+2y+z-6=0$ |
Gọi $(H)$ là hình phẳng giới hạn bởi parabol $(P)\colon y=2x-x^2$ và trục hoành. Đường thẳng $y=mx$ chia hình $(H)$ thành hai phần có diện tích bằng nhau. Tính giá trị $m$.
| $2-\sqrt[3]{4}$ | |
| $2-\sqrt{3}$ | |
| $2-\sqrt{4}$ | |
| $2-\sqrt[3]{5}$ |
Trong không gian $Oxyz$, tọa độ hình chiếu vuông góc của điểm $M(1;0;1)$ lên đường thẳng $\Delta\colon\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}$ là
| $\left(\dfrac{2}{7};\dfrac{4}{7};\dfrac{6}{7}\right)$ | |
| $(2;4;6)$ | |
| $(0;0;0)$ | |
| $\left(1;\dfrac{1}{2};\dfrac{1}{3}\right)$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon(x+3)^2+y^2+(z-1)^2=10$. Mặt phẳng nào trong các mặt phẳng dưới đây cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính bằng $3$?
| $\big(P_2\big)\colon x+2y-2z-8=0$ | |
| $\big(P_4\big)\colon x+2y-2z-4=0$ | |
| $\big(P_3\big)\colon x+2y-2z-2=0$ | |
| $\big(P_1\big)\colon x+2y-2z+8=0$ |
Trong không gian $Oxyz$, cho các vectơ $\overrightarrow{a}=(2;m-1;3)$, $\overrightarrow{b}=(1;3;-2n)$. Tìm $m,\,n$ để các vectơ $\overrightarrow{a},\,\overrightarrow{b}$ cùng phương.
| $m=7$; $n=\dfrac{3}{4}$ | |
| $m=1$; $n=0$ | |
| $m=4$; $n=-3$ | |
| $m=7$; $n=-\dfrac{3}{4}$ |
Gọi $A,\,B,\,C$ là điểm biểu diễn cho các số phức $z_1=-2+3i$, $z_2=-4-2i$, $z_3=3+i$. Khi đó tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $\left(-1;-\dfrac{2}{3}\right)$ | |
| $\left(-1;\dfrac{2}{3}\right)$ | |
| $\left(1;-\dfrac{2}{3}\right)$ | |
| $\left(1;\dfrac{2}{3}\right)$ |
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^2$ và đường thẳng $y=2x$ là
| $\dfrac{4}{3}$ | |
| $\dfrac{5}{3}$ | |
| $\dfrac{3}{2}$ | |
| $\dfrac{23}{15}$ |
Trong không gian $Oxyz$, cho mặt cầu có phương trình $x^2+y^2+z^2-2x+4y-6z+9=0$. Tọa độ tâm $I$ và bán kính $R$ của mặt cầu là
| $I(-1;2;-3)$ và $R=5$ | |
| $I(-1;2;-3)$ và $R=\sqrt{5}$ | |
| $I(1;-2;3)$ và $R=5$ | |
| $I(1;-2;3)$ và $R=\sqrt{5}$ |
Trong không gian $Oxyz$, cho ba điểm $A(2;1;-1)$, $B(-1;0;4)$, $C(0;-2;-1)$. Phương trình mặt phẳng đi qua $A$ và vuông góc với $BC$ là
| $x-2y-5z+5=0$ | |
| $x-2y-5=0$ | |
| $2x-y+5z-5=0$ | |
| $x-2y-5z-5=0$ |
Gọi $F(x)$ là một nguyên hàm của hàm số $f(x)=4x^3-3x+2$ thỏa mãn $F(-1)=-\dfrac{3}{2}$. Khi đó $F(x)$ bằng
| $x^4-\dfrac{3}{2}x^2+2x+2023$ | |
| $x^4-\dfrac{3}{2}x^2+2x-1$ | |
| $x^4-\dfrac{3}{2}x^2+2x+2$ | |
| $x^4-\dfrac{3}{2}x^2+2x+1$ |
Trong không gian $Oxyz$, cho hai mặt phẳng $(P)\colon2x+my-z+1=0$ và $(Q)\colon x+3y+(2m+3)z-2=0$. Giá trị của $m$ để $(P)\perp(Q)$ là
| $m=0$ | |
| $m=2$ | |
| $m=1$ | |
| $m=-1$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn cho số phức $z$.
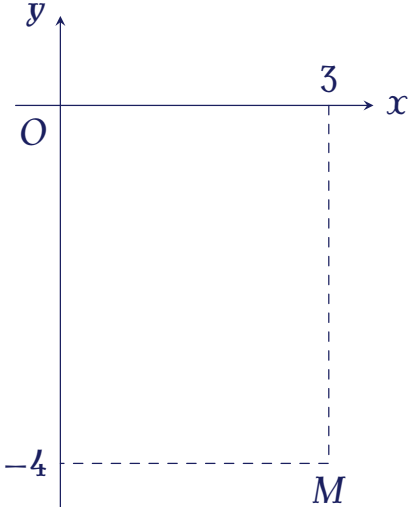
Phần ảo của số phức $(1+i)z$ bằng
| $7$ | |
| $-7$ | |
| $-1$ | |
| $1$ |
Tập hợp các số phức $z$ thỏa mãn $|z+1-2i|=3$ là đường tròn có tâm
| $I(-1;2)$ | |
| $I(-1;-2)$ | |
| $I(1;-2)$ | |
| $I(1;2)$ |
