Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên hợp với đáy một góc $60^\circ$. Gọi $M$ là điểm đối xứng với $C$ qua $D$, $N$ là trung điểm $SC$. Mặt phẳng $(BMN)$ chia khối chóp thành hai khối đa diện. Tính thể tích $V$ của khối đa diện chứa đỉnh $C$.
| $V=\dfrac{7\sqrt{6}a^3}{72}$ | |
| $V=\dfrac{7\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{72}$ |
Cho khối tứ diện $ABCD$. Hai điểm $M,\,N$ lần lượt là trung điểm của $BC$ và $BD$. Mặt phẳng $(AMN)$ chia khối tứ diện $ABCD$ thành
| Một khối tứ diện và một khối chóp tứ giác | |
| Hai khối chóp tứ giác | |
| Hai khối tứ diện | |
| Hai khối tứ diện và một khối chóp tứ giác |
Cho khối lập phương có cạnh bằng $2a$. Thể tích của khối lập phương đã cho bằng
| $\dfrac{8}{3}a^3$ | |
| $8a^3$ | |
| $4a^3$ | |
| $\dfrac{4}{3}a^3$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Khối đa diện đều như hình bên là khối đa diện nào sau đây?
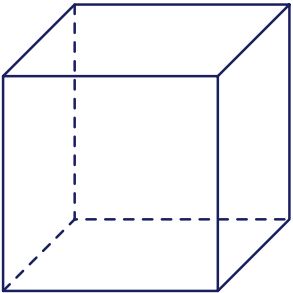
| Khối lập phương | |
| Khối tứ diện đều | |
| Khối mười hai mặt đều | |
| Khối bát diện đều |
Cho khối lập phương có cạnh bằng $2$. Thể tích của khối lập phương đã cho bằng
| $6$ | |
| $8$ | |
| $\dfrac{8}{3}$ | |
| $4$ |
Cho hình lập phương có tổng diện tích các mặt bằng $12a^2$. Tính theo $a$ thể tích khối lập phương đó.
| $\sqrt{2}a^3$ | |
| $a^3$ | |
| $2\sqrt{2}a^3$ | |
| $\dfrac{a^3}{3}$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Hình lập phương có số đỉnh, số cạnh và số mặt tương ứng là
| $12;8;6$ | |
| $8;6;12$ | |
| $6;12;8$ | |
| $8;12;6$ |
Khối đa diện đều loại $\{4,3\}$ có bao nhiêu mặt?
| $4$ | |
| $6$ | |
| $8$ | |
| $12$ |
Khối lập phương là khối đa diện loại
| $\{5,3\}$ | |
| $\{3,4\}$ | |
| $\{4,3\}$ | |
| $\{3,5\}$ |
Thể tích của khối lập phương cạnh $5a$ bằng
| $5a^3$ | |
| $a^3$ | |
| $125a^3$ | |
| $25a^3$ |
Cho hình chóp $S.ABCD$ có chiều cao bằng $8$ và đáy $ABCD$ là hình vuông cạnh bằng $3$. Gọi $M$ là trung điểm của $SB$ và $N$ là điểm thuộc $SD$ sao cho $\overrightarrow{SN}=2\overrightarrow{ND}$. Thể tích khối tứ diện $ACMN$ bằng
| $6$ | |
| $9$ | |
| $4$ | |
| $3$ |
Thể tích khối lập phương $ABCD.A'B'C'D'$ có đường chéo $AC'=2\sqrt{6}$ bằng
| $24\sqrt{3}$ | |
| $48\sqrt{6}$ | |
| $6\sqrt{6}$ | |
| $16\sqrt{2}$ |
Tính thể tích của khối gỗ có hình dạng dưới đây
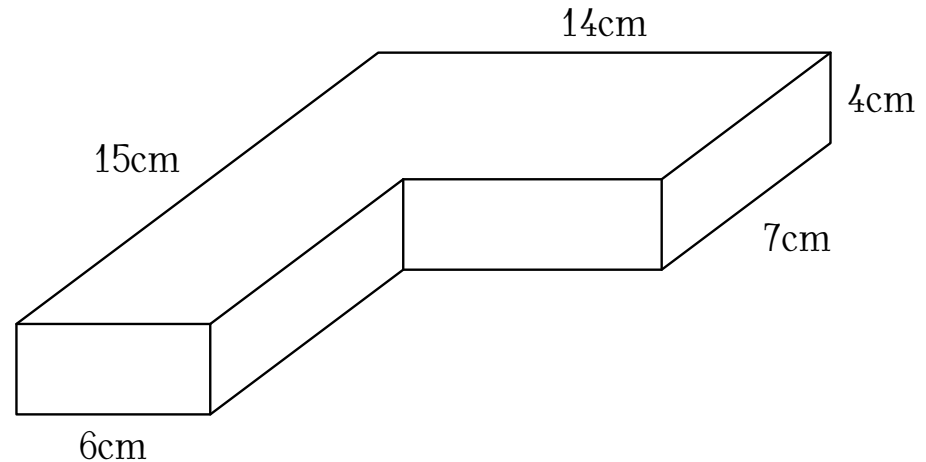
| $328$cm$^3$ | |
| $456$cm$^3$ | |
| $584$cm$^3$ | |
| $712$cm$^3$ |
Cho khối lăng trụ $ABC.A'B'C'$ có thể tích bằng $V$. Thể tích của khối đa diện $ABCC'B'$ bằng
| $\dfrac{3V}{4}$ | |
| $\dfrac{2V}{3}$ | |
| $\dfrac{V}{2}$ | |
| $\dfrac{V}{4}$ |
Cho khối chóp $S.ABCD$ có đáy là hình bình hành và có thể tích $48$. Trên các cạnh $SA,\,SB,\,SC,\,SD$ lần lượt lấy các điểm $A',\,B',\,C'$ và $D'$ sao cho $\dfrac{SA'}{SA}=\dfrac{SC'}{SC}=\dfrac{1}{3}$ và $\dfrac{SB'}{SB}=\dfrac{SD'}{SD}=\dfrac{3}{4}$. Tính thể tích $V$ của khối đa diện lõm $S.A'B'C'D'$.
| $V=4$ | |
| $V=9$ | |
| $V=\dfrac{3}{2}$ | |
| $V=6$ |
Tính thể tích khối rubic lập phương có cạnh bằng $8$cm (Bỏ các khe hở của khối rubic, xem thể tích của khe hở không đáng kể).
| $24\,\mathrm{cm}^3$ | |
| $8\,\mathrm{cm}^3$ | |
| $512\,\mathrm{cm}^3$ | |
| $\dfrac{512}{3}\,\mathrm{cm}^3$ |
