Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=x^{2}+10x$, $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=f\left(x^4-8x^2+m\right)$ có đúng $9$ điểm cực trị?
| $16$ | |
| $9$ | |
| $15$ | |
| $10$ |
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon(x-4)^2+(y+3)^2+(z+6)^2=50$ và đường thẳng $d\colon\dfrac{x}{2}=\dfrac{y+2}{4}=\dfrac{z-3}{-1}$. Có bao nhiêu điểm $M$ thuộc trục hoành, với hoành độ là số nguyên, mà từ $M$ kẻ được đến $(S)$ hai tiếp tuyến cùng vuông góc với $d$?
| $29$ | |
| $33$ | |
| $55$ | |
| $28$ |
Có bao nhiêu số nguyên $a$ sao cho ứng với mỗi $a$, tồn tại ít nhất bốn số nguyên $b\in(-12;12)$ thỏa mãn $4^{a^2+b}\leq3^{b-a}+65$?
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
Cho khối nón đỉnh $S$ có bán kính đáy bằng $2\sqrt{3}a$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho $AB=4a$. Biết khoảng cách từ tâm của đáy đến mặt phẳng $(SAB)$ bằng $2a$, thể tích của khối nón đã cho bằng
| $\dfrac{8\sqrt{2}}{3}\pi a^3$ | |
| $4\sqrt{6}\pi a^3$ | |
| $\dfrac{16\sqrt{3}}{3}\pi a^3$ | |
| $8\sqrt{2}\pi a^3$ |
Trong không gian $Oxyz$, cho điểm $A(-4;-3;3)$ và mặt phẳng $(P)\colon x+y+z=0$. Đường thẳng đi qua $A$, cắt trục $Oz$ và song song với $(P)$ có phương trình là
| $\dfrac{x-4}{4}=\dfrac{y-3}{3}=\dfrac{z-3}{-7}$ | |
| $\dfrac{x+4}{4}=\dfrac{y+3}{3}=\dfrac{z-3}{1}$ | |
| $\dfrac{x+4}{-4}=\dfrac{y+3}{3}=\dfrac{z-3}{1}$ | |
| $\dfrac{x+8}{4}=\dfrac{y+6}{3}=\dfrac{z-10}{-7}$ |
Cho hàm số $f(x)=3x^4+ax^3+bx^2+cx+d$ $(a,\,b,\,c,\,d\in\mathbb{R})$ có ba điểm cực trị là $-2,\,-1$ và $1$. Gọi $y=g(x)$ là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $\dfrac{500}{81}$ | |
| $\dfrac{36}{5}$ | |
| $\dfrac{2932}{405}$ | |
| $\dfrac{2948}{405}$ |
Gọi $S$ là tập hợp tất cả các số phức $z$ sao cho số phức $w=\dfrac{1}{|z|-z}$ có phần thực bằng $\dfrac{1}{8}$. Xét các số phức $z_1,\,z_2\in S$ thỏa mãn $\left|z_1-z_2\right|=2$, giá trị lớn nhất của $P=\left|z_1-5i\right|^2-\left|z_2-5i\right|^2$ bằng
| $16$ | |
| $20$ | |
| $10$ | |
| $32$ |
Trên tập hợp các số phức, xét phương trình $z^2-2mz+8m-12=0$ ($m$ là tham số thực). Có bao nhiêu giá trị nguyên của $m$ để phương trình đó có hai nghiệm phân biệt $z_1,\,z_2$ thỏa mãn $\left|z_1\right|=\left|z_2\right|$?
| $5$ | |
| $6$ | |
| $3$ | |
| $4$ |
Cho khối chóp đều $S.ABCD$ có $AC=4a$, hai mặt phẳng $(SAB)$ và $(SCD)$ vuông góc với nhau. Thể tích của khối chóp đã cho bằng
| $\dfrac{16\sqrt{2}}{3}a^3$ | |
| $\dfrac{8\sqrt{2}}{3}a^3$ | |
| $16a^3$ | |
| $\dfrac{16}{3}a^3$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=12x^2+2$, $\forall x\in\mathbb{R}$ và $f(1)=3$. Biết $F(x)$ là nguyên hàm của $f(x)$ thỏa mãn $F(0)=2$, khi đó $F(1)$ bằng
| $-3$ | |
| $1$ | |
| $2$ | |
| $7$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Số nghiệm thực phân biệt của phương trình $f'\left(f(x)\right)=0$ là
| $3$ | |
| $4$ | |
| $5$ | |
| $6$ |
Có bao nhiêu số nguyên $x$ thỏa mãn $\left(4^x-5\cdot2^{x+2}+64\right)\sqrt{2-\log(4x)}\geq0$?
| $22$ | |
| $25$ | |
| $23$ | |
| $24$ |
Trong không gian $Oxyz$, cho ba điểm $A(2;-2;3)$, $B(1;3;4)$ và $C(3;-1;5)$. Đường thẳng đi qua $A$ và song song với $BC$ có phương trình là
| $\dfrac{x-2}{2}=\dfrac{y+4}{-2}=\dfrac{z-1}{3}$ | |
| $\dfrac{x+2}{2}=\dfrac{y-2}{-4}=\dfrac{z+3}{1}$ | |
| $\dfrac{x-2}{4}=\dfrac{y+2}{2}=\dfrac{z-3}{9}$ | |
| $\dfrac{x-2}{2}=\dfrac{y+2}{-4}=\dfrac{z-3}{1}$ |
Từ một hộp chứa $16$ quả cầu gồm $7$ quả màu đỏ và $9$ quả màu xanh, lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được hai quả có màu khác nhau bằng
| $\dfrac{7}{40}$ | |
| $\dfrac{21}{40}$ | |
| $\dfrac{3}{10}$ | |
| $\dfrac{2}{15}$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$ và $AB=4$ (tham khảo hình bên).
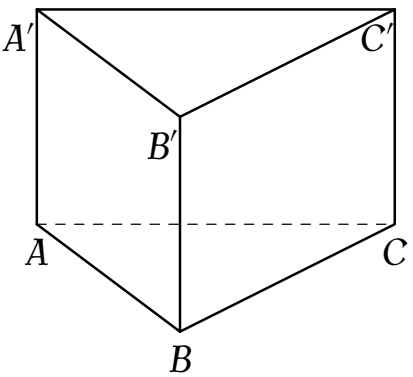
Khoảng cách từ $C$ đến mặt phẳng $\left(ABB'A'\right)$ bằng
| $2\sqrt{2}$ | |
| $2$ | |
| $\sqrt{2}$ | |
| $4$ |
Cho số phức $z$ thỏa mãn $i\overline{z}=5+2i$. Phần ảo của $z$ bằng
| $5$ | |
| $2$ | |
| $-5$ | |
| $-2$ |
Trong không gian $Oxyz$, cho điểm $M(2;-5;3)$ và đường thẳng $d\colon\dfrac{x}{2}=\dfrac{y+2}{4}=\dfrac{z-3}{-1}$. Mặt phẳng đi qua $M$ và vuông góc với $d$ có phương trình là
| $2x-5y+3z-38=0$ | |
| $2x+4y-z+19=0$ | |
| $2x+4y-z-19=0$ | |
| $2x+4y-z+11=0$ |
Nếu $\displaystyle\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x=2$ thì $\displaystyle\displaystyle\int\limits_{1}^{3}[f(x)+2x]\mathrm{\,d}x$ bằng
| $20$ | |
| $10$ | |
| $18$ | |
| $12$ |
Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
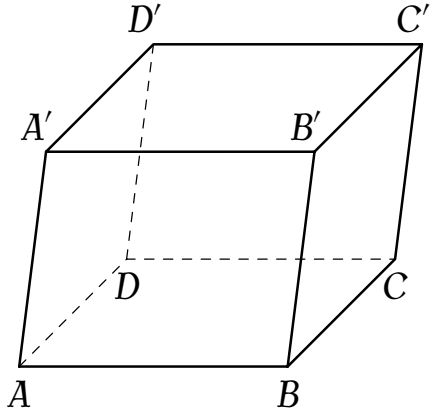
Góc giữa hai đường thẳng $A'C'$ và $BD$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Với mọi $a,\,b$ thỏa mãn $\log_2a-3\log_2b=2$, khẳng định nào dưới đây đúng?
| $a=4b^3$ | |
| $a=3b+4$ | |
| $a=3b+2$ | |
| $a=\dfrac{4}{b^3}$ |
