Gọi $x_0$ là nghiệm dương nhỏ nhất của phương trình $2\sin^2x+\sin x-1=0$. Mệnh đề nào sau đây là đúng?
| $x_0\in\left[\dfrac{5\pi}{6};\dfrac{3\pi}{2}\right]$ | |
| $x_0\in\left(\dfrac{\pi}{6};\dfrac{5\pi}{6}\right)$ | |
| $x_0\in\left(0;\dfrac{\pi}{4}\right)$ | |
| $x_0\in\left(\dfrac{\pi}{2};\pi\right)$ |
Gọi $M,\,m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y=3\sin x+4\cos x+1$. Khẳng định nào sau đây đúng?
| $M=5,\,m=-5$ | |
| $M=-8,\,m=-6$ | |
| $M=6,\,m=-2$ | |
| $M=6,\,m=-4$ |
Tập nghiệm của phương trình $2\sin^2x-\sin2x=0$ có tập nghiệm là
| $\left\{\dfrac{\pi}{4}+k2\pi|k\in\mathbb{Z}\right\}$ | |
| $\left\{k2\pi|k\in\mathbb{Z}\right\}$ | |
| $\left\{k\pi|k\in\mathbb{Z}\right\}$ | |
| $\left\{\dfrac{\pi}{4}+k\pi;\,\, k\pi |k\in\mathbb{Z}\right\}$ |
Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\sin x-\cos x+3$. Tính $M\cdot m$.
| $7$ | |
| $-4$ | |
| $-7$ | |
| $6$ |
Tìm tất cả các giá trị của tham số $m$ để phương trình $\sin x+\left(m-1\right)\cos x=2m-1$ có nghiệm.
| $\dfrac{1}{3}\le m\le\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}\le m\le\dfrac{1}{3}$ | |
| $-\dfrac{1}{3}\le m\le1$ | |
| $\dfrac{1}{2}\le m\le1$ |
Số nghiệm của phương trình $\sin x-\sqrt{3}\cos x=2$ trong khoảng $\left(0;5\pi\right)$ là
| $3$ | |
| $4$ | |
| $2$ | |
| $1$ |
Nghiệm dương lớn nhất của phương trình $5\sin x-\cos2x-2=0$ trên đoạn $[0;2\pi]$ là
| $\dfrac{5\pi}{6}$ | |
| $\dfrac{2\pi}{3}$ | |
| $\dfrac{\pi}{6}$ | |
| $\dfrac{\pi}{3}$ |
Phương trình $\sin x-\sqrt{3}\cos x=2$ có tập nghiệm là
| $S=\left\{x=-\dfrac{\pi}{6}+k\pi\left|k\in\mathbb{Z}\right.\right\}$ | |
| $S=\left\{x=\dfrac{5\pi}{6}+k2\pi\left|k\in\mathbb{Z}\right.\right\}$ | |
| $S=\left\{x=\dfrac{5\pi}{6}+k\pi\left|k\in\mathbb{Z}\right.\right\}$ | |
| $S=\left\{x=\dfrac{\pi}{6}+k2\pi\left|k\in\mathbb{Z}\right.\right\}$ |
Cho hàm số $y=\dfrac{\sin x-\cos x+\sqrt{2}}{\sin x+\cos x+2}$. Giả sử hàm số có giá trị lớn nhất là $M$, giá trị nhỏ nhất là $N$. Khi đó, giá trị của $2M+N$ là
| $4\sqrt{2}$ | |
| $2\sqrt{2}$ | |
| $4$ | |
| $\sqrt{2}$ |
Tập giá trị của hàm số $y=5\sin x-12\cos x$ là
| $[-12;5]$ | |
| $[-13;13]$ | |
| $[-17;17]$ | |
| $(-13;13)$ |
Một chiếc cổng hình parabol dạng $y=-\dfrac{1}{2}x^2$ có chiều rộng chân cổng $d=8$m (như hình).
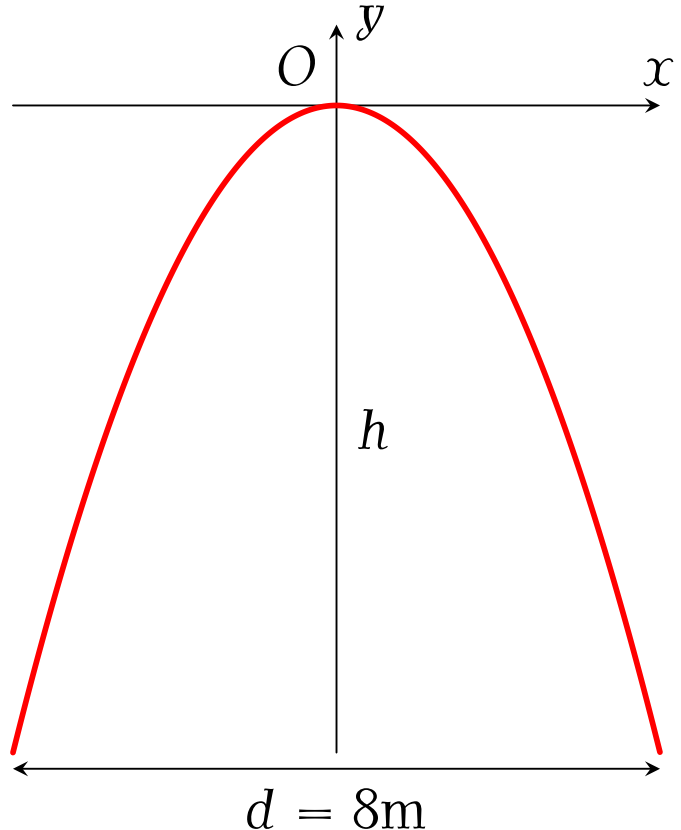
Hãy tính chiều cao $h$ của cổng.
| $h=8$m | |
| $h=9$m | |
| $h=7$m | |
| $h=5$m |
Một vật chuyển động trong $3$ giờ với vận tốc $v$ (km/h) phụ thuộc thời gian $t$ (h) có đồ thị là một phần của đường parabol với đỉnh $I(2;9)$ và trục đối xứng song song với trục tung (như hình vẽ).
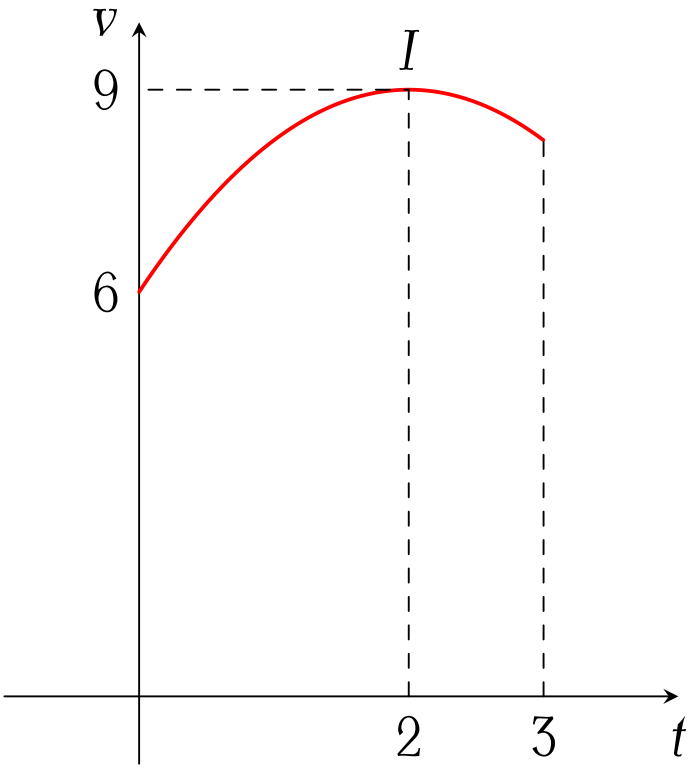
Vận tốc tức thời của vật tại thời điểm $2$ giờ $30$ phút sau khi vật bắt đầu chuyển động gần bằng giá trì nào nhất trong các giá trị sau:
| $8,7$ (km/h) | |
| $8,8$ (km/h) | |
| $8,6$ (km/h) | |
| $8,5$ (km/h) |
Cho hàm số $y=-x^2+4x+1$. Khẳng định nào sau đây sai?
| Hàm số nghịch biến trên khoảng $(2;+\infty)$ và đồng biến trên khoảng $(-\infty;2)$ | |
| Hàm số nghịch biến trên khoảng $(4;+\infty)$ và đồng biến trên khoảng $(-\infty;4)$ | |
| Hàm số đồng biến trên khoảng $(-\infty;-1)$ | |
| Hàm số nghịch biến trên khoảng $(3;+\infty)$ |
Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
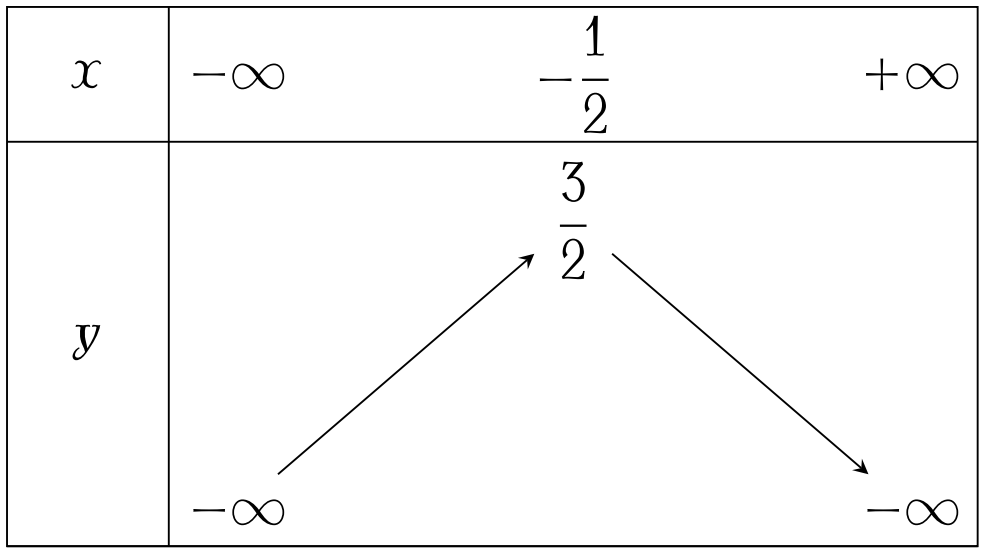
| $y=2x^2+2x-1$ | |
| $y=2x^2+2x+2$ | |
| $y=-2x^2-2$ | |
| $y=-2x^2-2x+1$ |
Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
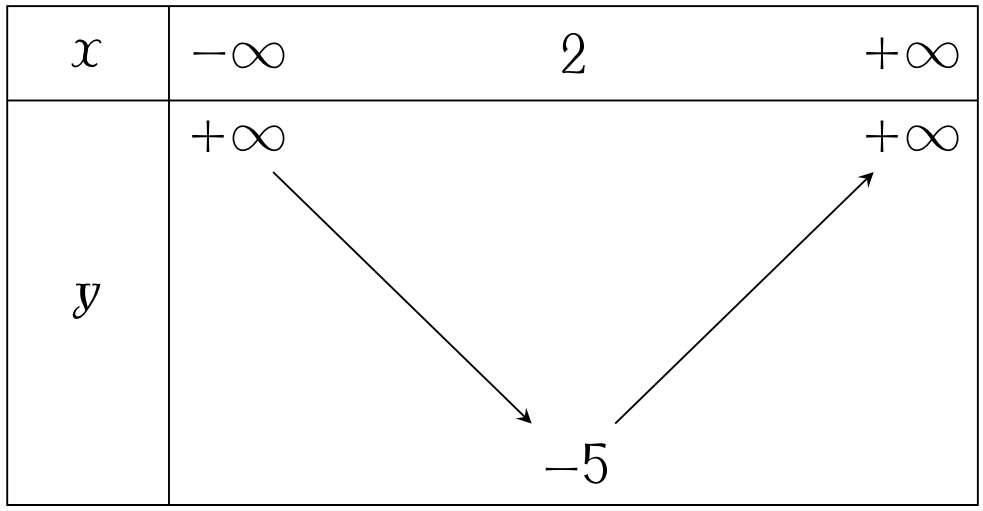
| $y=-x^2+4x-9$ | |
| $y=x^2-4x-1$ | |
| $y=-x^2+4x$ | |
| $y=x^2-4x-5$ |
Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
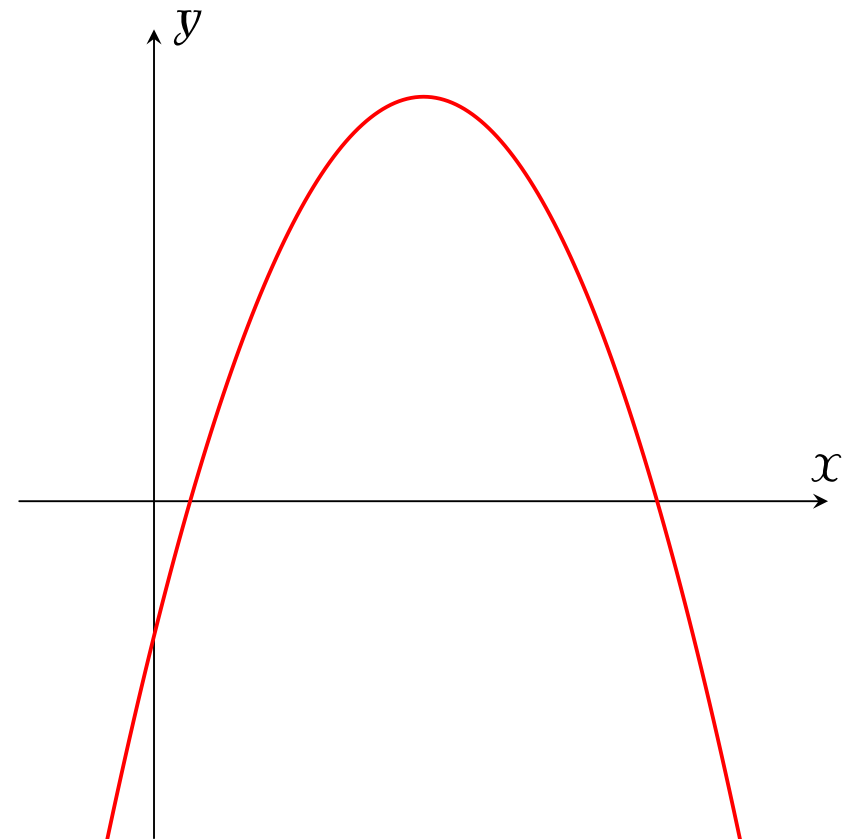
| $a>0,\,b>0,\,c<0$ | |
| $a>0,\,b<0,\,c>0$ | |
| $a<0,\,b>0,\,c<0$ | |
| $a<0,\,b>0,\,c>0$ |
Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
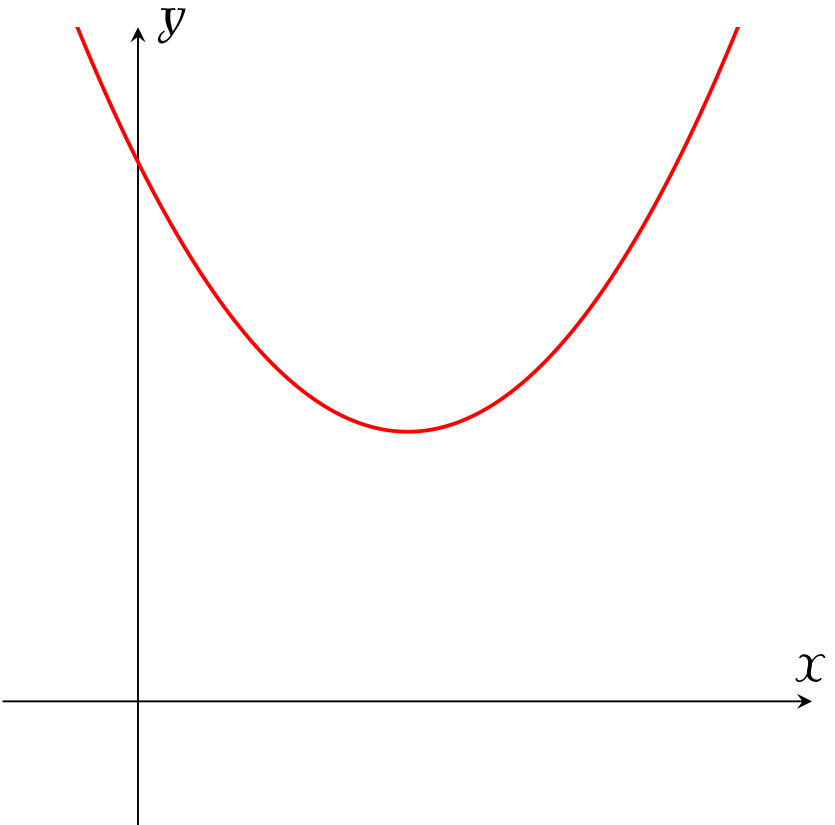
| $a>0,\,b<0,\,c<0$ | |
| $a>0,\,b<0,\,c>0$ | |
| $a>0,\,b>0,\,c>0$ | |
| $a<0,\,b<0,\,c>0$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
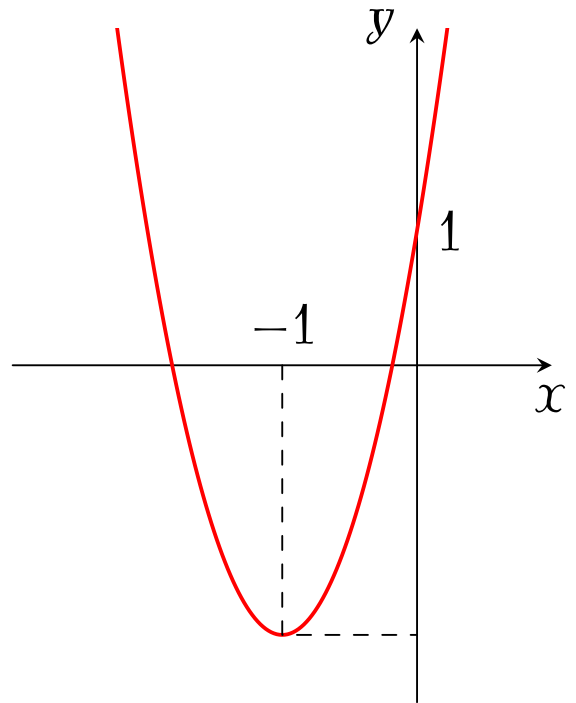
| $y=-3x^2-6x$ | |
| $y=3x^2+6x+1$ | |
| $y=x^2+2x+1$ | |
| $y=-x^2-2x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
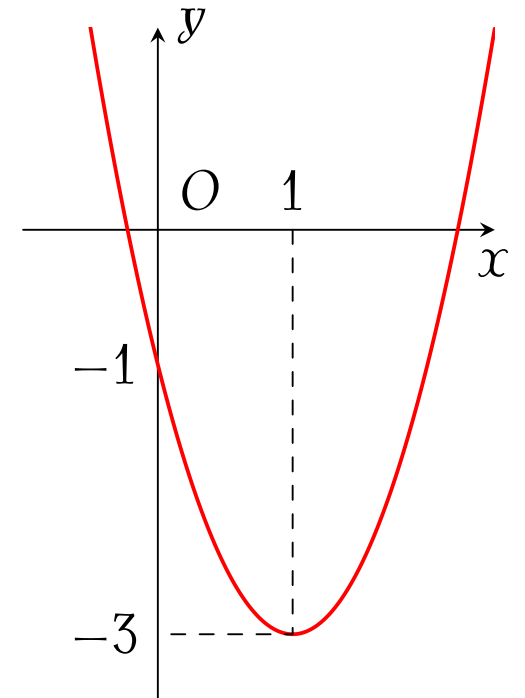
| $y=x^2-4x-1$ | |
| $y=2x^2-4x-1$ | |
| $y=-2x^2-4x-1$ | |
| $y=2x^2-4x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
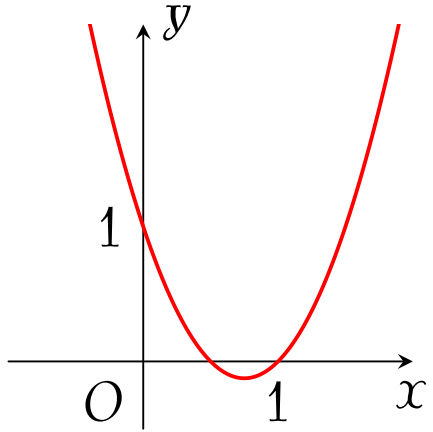
| $y=-x^2+3x-1$ | |
| $y=-2x^2+3x-1$ | |
| $y=2x^2-3x+1$ | |
| $y=x^2-3x+1$ |
