Có bao nhiêu số thực $x$ thỏa mãn $9^{\log_3x}=4$?
| $4$ | |
| $0$ | |
| $2$ | |
| $1$ |
Tập nghiệm $S$ của phương trình $2^{x+1}=8$ là
| $S=\{4\}$ | |
| $S=\{1\}$ | |
| $S=\{3\}$ | |
| $S=\{2\}$ |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\log_2\left(x^2-2x+m\right)$ có tập xác định là $\mathbb{R}$.
| $m\geq1$ | |
| $m\leq1$ | |
| $m>1$ | |
| $m< -1$ |
Ông A dự định gửi vào ngân hàng một số tiền với lãi suất $7,5\%$ một năm, để sau $5$ năm, số tiền lãi đủ mua một chiếc xe máy trị giá $85$ triệu đồng. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Hỏi số tiền ông A cần gửi cho ngân hàng gần nhất với số tiền nào dưới đây?
| $60$ triệu đồng | |
| $189$ triệu đồng | |
| $196$ triệu đồng | |
| $210$ triệu đồng |
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án $A,\,B,\,C,\,D$ dưới đây.
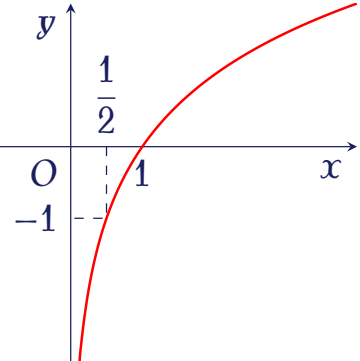
Hỏi hàm số đó là hàm số nào?
| $y=\log_2x$ | |
| $y=\log_{\sqrt{2}}x$ | |
| $y=\log_22x$ | |
| $y=\log_{\tfrac{1}{2}}x$ |
Cho $\log_25=a$ và $\log_35=b$. Khi đó, $\log_65$ tính theo $a$ và $b$ là
| $a^2+b^2$ | |
| $\dfrac{ab}{a+b}$ | |
| $\dfrac{1}{a+b}$ | |
| $a+b$ |
Với $\log3=a$ thì $\log9000$ được biểu diễn theo $a$ bằng
| $a^2$ | |
| $3+2a$ | |
| $a^2+3$ | |
| $3a^2$ |
Cho các số thực dương $a,\,b$ với $a\neq1$. Khẳng định nào sau đây là khẳng định đúng?
| $\log_{a^2}(ab)=2+\log_ab$ | |
| $\log_{a^2}(ab)=\dfrac{1}{2}\log_ab$ | |
| $\log_{a^2}(ab)=\dfrac{1}{2}+\dfrac{1}{2}\log_ab$ | |
| $\log_{a^2}(ab)=\dfrac{1}{4}\log_ab$ |
Tìm mệnh đề đúng trong các mệnh đề sau:
| Đồ thị hàm số $y=a^x$ và $y=\left(\dfrac{1}{a}\right)^x$ với $0< a\neq1$ đối xứng với nhau qua trục $Oy$ | |
| Đồ thị hàm số $y=a^x$ với $0< a\neq1$ luôn đi qua điểm $(a;1)$ | |
| Hàm số $y=a^x$ với $a>1$ nghịch biến trên $(-\infty;+\infty)$ | |
| Hàm số $y=a^x$ với $0< a< 1$ đồng biến trên $(-\infty;+\infty)$ |
Hàm số $f(x)=\left(x^2+2x\right)\mathrm{e}^{-x}$ có đạo hàm
| $f'(x)=\left(x^2+4x+2\right)\mathrm{e}^{-x}$ | |
| $f'(x)=\left(2x+2\right)\mathrm{e}^{-x}$ | |
| $f'(x)=\left(-2x+2\right)\mathrm{e}^{-x}$ | |
| $f'(x)=\left(-x^2+2\right)\mathrm{e}^{-x}$ |
Cho các số thực $a,\,b$ thỏa $\left(\sqrt{2019}-\sqrt{2018}\right)^a>\left(\sqrt{2019}-\sqrt{2018}\right)^b$. Kết luận nào sau đây đúng?
| $a>b$ | |
| $a< b$ | |
| $a=b$ | |
| $a\geq b$ |
Cho $P=\left(5-2\sqrt{6}\right)^{2018}\left(5+2\sqrt{6}\right)^{2019}$. Ta có
| $P\in(3;7)$ | |
| $P\in(7;9)$ | |
| $P\in(9;10)$ | |
| $P\in(10;11)$ |
Cho $a$ là số thực dương. Biểu thức $a^2\cdot\sqrt[3]{a}$ được viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $a^{\tfrac{4}{3}}$ | |
| $a^{\tfrac{7}{3}}$ | |
| $a^{\tfrac{5}{3}}$ | |
| $a^{\tfrac{2}{3}}$ |
Có bao nhiêu giá trị của $m$ để đồ thị của hàm số $y=\dfrac{x}{1-x}$ cắt đường thẳng $y=x-m$ tại hai điểm phân biệt $A,\,B$ sao cho góc giữa hai đường thẳng $OA$ và $OB$ bằng $60^\circ$ ($O$ là gốc tọa độ)?
| $2$ | |
| $1$ | |
| $3$ | |
| $0$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{-1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.
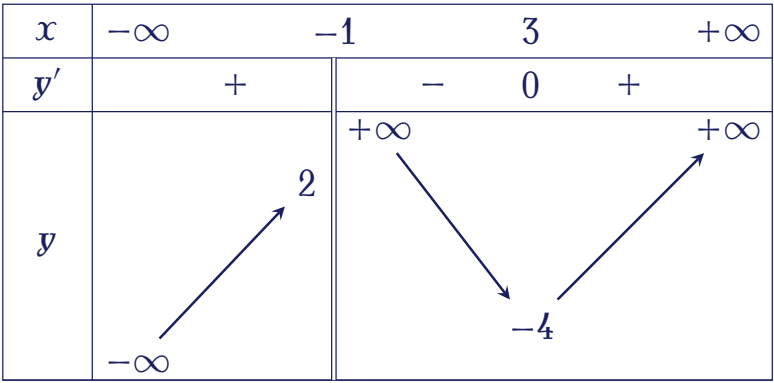
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho phương trình $f(x)=m$ có đúng ba nghiệm thực phân biệt.
| $(-4;2)$ | |
| $[-4;2)$ | |
| $(-4;2]$ | |
| $(-\infty;2]$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như hình vẽ bên.
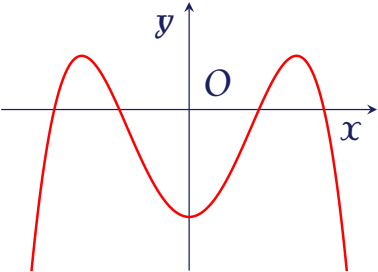
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b>0,\,c< 0$ | |
| $a>0,\,b< 0,\,c>0$ |
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
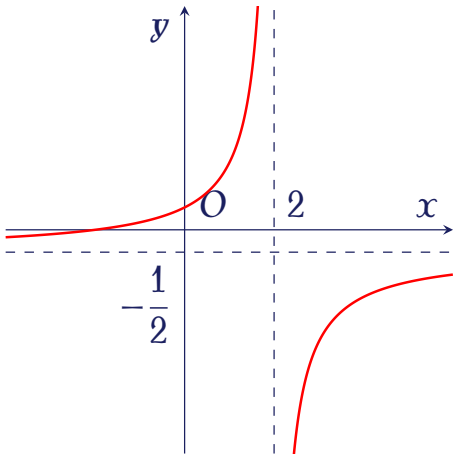
| $y=\dfrac{x+2}{-2x+4}$ | |
| $y=\dfrac{-x+1}{x-2}$ | |
| $y=\dfrac{2x-3}{x+2}$ | |
| $y=\dfrac{-x+3}{2x-4}$ |
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
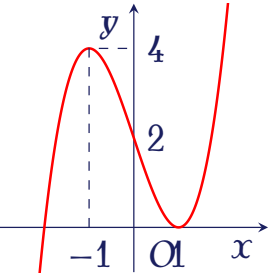
| $y=-x^3+3x+2$ | |
| $y=x^3-2x+2$ | |
| $y=x^3-3x+2$ | |
| $y=x^3+3x+2$ |
Cho hàm số $y=\dfrac{x+b}{cx-1}$ có đồ thị như hình bên.
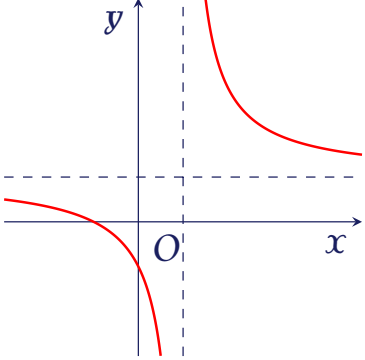
Mệnh đề nào dưới đây là đúng?
| $b< 0,\,c< 0$ | |
| $b< 0,\,c>0$ | |
| $b>0,\,c>0$ | |
| $b>0,\,c< 0$ |
Cho hàm số $y=\dfrac{x}{x-1}+2$ có đồ thị $\left(\mathscr{C}\right)$ Mệnh đề nào dưới đây đúng?
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=1$ | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=3$ | |
| Đồ thị $\left(\mathscr{C}\right)$ không có tiệm cận | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận đứng $x=2$ |
