Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(xf\left(x^3\right)+f\left(1-x^2\right)=-x^{10}+x^6-2x\), \(\forall x\in\mathbb{R}\). Khi đó \(\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x\) bằng

	\(-\dfrac{17}{20}\)
	\(-\dfrac{13}{4}\)
	\(\dfrac{17}{4}\)
	\(-1\)

Có bao nhiêu cặp số nguyên \((x;y)\) thỏa mãn \(0\leq x\leq2020\) và \(\log_3(3x+3)+x=2y+9^y\)?

	\(2019\)
	\(6\)
	\(2020\)
	\(4\)

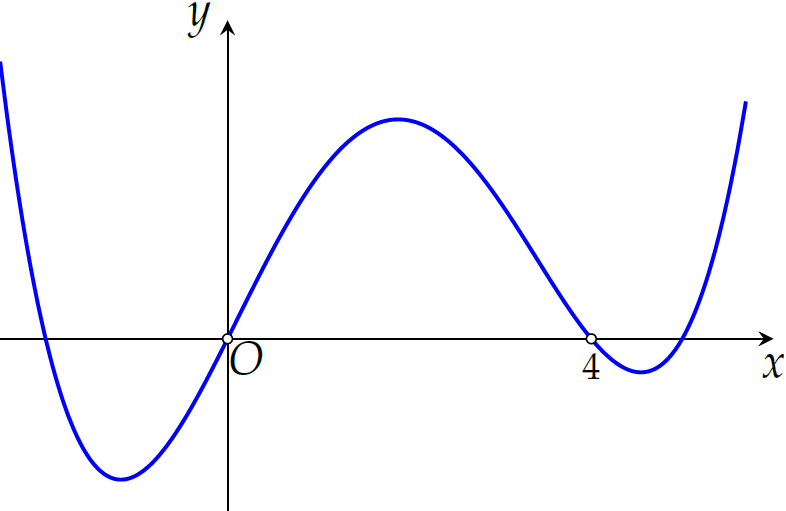
Cho hàm số bậc bốn \(y=f(x)\) có đồ thị như hình trên. Số điểm cực trị của hàm số \(g(x)=f\left(x^3+3x^2\right)\) là

	\(5\)
	\(3\)
	\(7\)
	\(11\)

Cho hàm số \(f(x)\) có bảng biến thiên như sau:

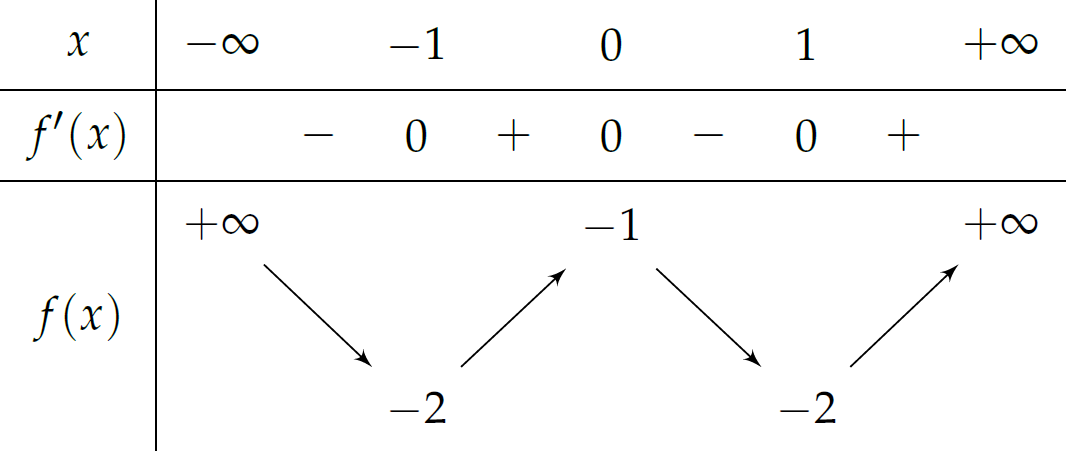
Số nghiệm thuộc đoạn \(\left[-\pi;2\pi\right]\) của phương trình \(2f\left(\sin x\right)+3=0\) là

	\(4\)
	\(6\)
	\(3\)
	\(8\)

Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\). Biết \(\cos2x\) là một nguyên hàm của hàm số \(f(x)\cdot\mathrm{e}^x\), họ tất cả các nguyên hàm của hàm số \(f'(x)\mathrm{e}^x\) là

	\(-\sin2x+\cos2x+C\)
	\(-2\sin2x+\cos2x+C\)
	\(-2\sin2x-\cos2x+C\)
	\(2\sin2x-\cos2x+C\)

Cho phương trình \(\log_2^2(2x)-(m+2)\log_2x+m-2=0\) (\(m\) là tham số thực). Tập hợp tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn \([1;2]\) là

	\(\left(1;2\right)\)
	\(\left[1;2\right]\)
	\(\left[1;2\right)\)
	\(\left[2;+\infty\right)\)

Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f(x)=\left|x^3-3x+m\right|\) trên đoạn \(\left[0;3\right]\) bằng \(16\). Tổng tất cả các phần tử của \(S\) bằng

	\(-16\)
	\(16\)
	\(-12\)
	\(-2\)

Cho \(x,\,y\) là các số thực dương thỏa mãn $$\log_9x=\log_6y=\log_4\left(2x+y\right)$$Giá trị của \(\dfrac{x}{y}\) bằng

	\(2\)
	\(\dfrac{1}{2}\)
	\(\log_2\left(\dfrac{3}{2}\right)\)
	\(\log_{\tfrac{3}{2}}2\)

Trong không gian \(Oxyz\), mặt phẳng đi qua điểm \(M\left(1;1;-1\right)\) và vuông góc với đường thẳng \(\Delta\colon\dfrac{x+1}{2}=\dfrac{y-2}{2}=\dfrac{z-1}{1}\) có phương trình là

	\(2x+2y+z+3=0\)
	\(x-2y-z=0\)
	\(2x+2y+z-3=0\)
	\(x-2y-z-2=0\)

Trong không gian \(Oxyz\), điểm nàọ dưới đây thuộc đường thẳng \(d\colon\dfrac{x+1}{-1}=\dfrac{y-2}{3}=\dfrac{z-1}{3}\)?

	\(P\left(-1;2;1\right)\)
	\(Q\left(1;-2;-1\right)\)
	\(N\left(-1;3;2\right)\)
	\(M\left(1;2;1\right)\)

Trong không gian \(Oxyz\), vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm \(M\left(2;3;-1\right)\) và \(N\left(4;5;3\right)\)?

	\(\overrightarrow{u_4}=\left(1;1;1\right)\)
	\(\overrightarrow{u_3}=\left(1;1;2\right)\)
	\(\overrightarrow{u_1}=\left(3;4;1\right)\)
	\(\overrightarrow{u_2}=\left(3;4;2\right)\)

Trong không gian \(Oxyz\), cho mặt phẳng \(\left(\alpha\right)\colon3x+2y-4z+1=0\). Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left(\alpha\right)\)?

	\(\overrightarrow{n_2}=\left(3;2;4\right)\)
	\(\overrightarrow{n_3}=\left(2;-4;1\right)\)
	\(\overrightarrow{n_1}=\left(3;-4;1\right)\)
	\(\overrightarrow{n_4}=\left(3;2;-4\right)\)

Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\) có tâm là điểm \(I\left(0;0;-3\right)\) và đi qua điểm \(M\left(4;0;0\right)\). Phương trình của \(\left(S\right)\) là

	\(x^2+y^2+\left(z+3\right)^2=25\)
	\(x^2+y^2+\left(z+3\right)^2=5\)
	\(x^2+y^2+\left(z-3\right)^2=25\)
	\(x^2+y^2+\left(z-3\right)^2=5\)

Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\colon\left(x-1\right)^2+\left(y+2\right)^2+\left(z-3\right)^2=16\). Tâm của \(\left(S\right)\) có tọa độ là

	\(\left(-1;-2;-3\right)\)
	\(\left(1;2;3\right)\)
	\(\left(-1;2;-3\right)\)
	\(\left(1;-2;3\right)\)

Trong không gian \(Oxyz\), cho các vectơ \(\vec{a}=\left(1;0;3\right)\) và \(\vec{b}=\left(-2;2;5\right)\). Tích vô hướng \(\vec{a}\cdot\left(\vec{a}+\vec{b}\right)\) bằng

	\(25\)
	\(23\)
	\(27\)
	\(29\)

Trong không gian \(Oxyz\), hình chiếu của điểm \(M\left(2;-2;1\right)\) trên mặt phẳng \((Oxy)\) có tọa độ là

	\(\left(2;0;1\right)\)
	\(\left(2;-2;0\right)\)
	\(\left(0;-2;1\right)\)
	\(\left(0;0;1\right)\)

Cho hình nón có chiều cao bằng \(2\sqrt{5}\). Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng \(9\sqrt{3}\). Thể tích của khối nón giới hạn bởi hình nón đã cho bằng

	\(\dfrac{32\sqrt{5}\pi}{3}\)
	\(32\pi\)
	\(32\sqrt{5}\pi\)
	\(96\pi\)

Cho hình trụ có bán kính đáy bằng \(3\). Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng

	\(18\pi\)
	\(36\pi\)
	\(54\pi\)
	\(27\pi\)

Diện tích xung quanh của hình nón có độ dài đường sinh \(l\) và bán kính đáy \(r\) bằng

	\(4\pi rl\)
	\(2\pi rl\)
	\(\pi rl\)
	\(\dfrac{1}{3}\pi rl\)

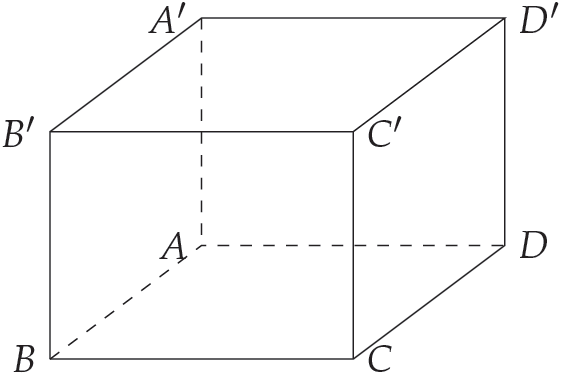
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(BD=a\sqrt{3}\), \(AA'=4a\) (minh họa như hình trên). Thể tích của khối lăng trụ đã cho bằng

	\(2\sqrt{3}a^3\)
	\(4\sqrt{3}a^3\)
	\(\dfrac{2\sqrt{3}a^3}{3}\)
	\(\dfrac{4\sqrt{3}a^3}{3}\)